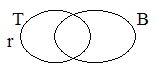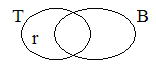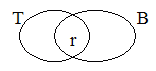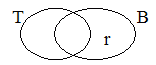Deductive Logic
I've tried teaching deductive logic by starting with the correct
definition of validity, and it doesn't
work. So although this chapter will give the
correct definition, we will work with a
simplified, heuristic definition for this
chapter, and then work with all the weird consequences of the correct
definition next chapter.
Here are some examples of deductive arguments.
1. No
fallacy is a logically compelling argument. Your argument is a fallacy,
so it's not a logically compelling argument.
2. Sam is either a monkey or a supermodel. He's not a supermodel, so
he's a monkey.
3. If you're a toad, you eat woad. You don't eat woad, so you sure
ain't a toad.
4. Cheese is a mineral, and cheese is not a mineral, so cheese both is
and is not a mineral
5. Joe is a Frenchman and an onion seller, so we do know he sells
onions.
You're a fish. All fish are flyers. So, you're a flyer and a fish.
6. If you're a cat, you're a dog. If you're a dog, you're a rat. So if
you're a cat, you're a rat.
Notice how simplistic and pointless they are? It's true I
chose some simple and silly examples to introduce you to deductive
logic, but you should know that even the most serious and complicated
deductive arguments will have the same flavor of pointlessness as the
examples given above.
Notice also that none of these arguments
refer in any way to our experience of the world.
The first one makes a sweeping generalization, but does not back it up
with any kind of sample. The second one just stipulates that
"Sam," whoever he is, has to be either one thing
or another. The third makes a broad claim about all toads, but again
without giving any evidence, and so on. This is because deductive logic
is fundamentally about concepts. It concerns
relationships between concepts and the applicability of various
concepts to various objects. It's incredibly useful, perhaps even vital
to reasoning, but in itself it is not the kind of reasoning that gives
you knowledge about the existance or nonexistance of objects in the
world.
Deductive logic is fundamentally different from inductive
logic. The rules that work for inductive reasoning don't really apply
to deductive logic, and vice versa. That's the basic idea I want to get
across in this chapter. The true depth and weirdness of deductive logic
can wait until next chapter.
Deductive arguments can't also be inductive. If it's
inductive, it's not deductive. If it's deductive, it's not inductive.
And there's no third kind of logic, so every argument is either
inductive or deductive. Every argument is one
kind or the other, but no argument is both kinds, and there are no
arguments that are neither kind.
This chapter also cover the difference between deductive and
inductive logic, which is also a little bit weird, but also can be easy
to master if you're willing to bite the bullet
and embrace -- well, accept -- okay, tolerate -- the weirdness of it.
One big problem with teaching the difference between deductive
and inductive arguments is that there are certain teachers out there
who have memorized a false definition of
that difference and who then mindlessly "teach" that false
definition to their students. If you have ever been taught a definition
of deductive that is substantially different from
the one given below, you should work very hard to forget
it. If it says something different from the definition
given in this chapter, it is completely false,
and relying on it will make you give wrong answers to the quiz.
Don't worry if you have trouble with these concepts at first.
Most people do, and be assured that I'm going to do my best to make
them as clear as possible. Indeed, you might find that you get the
concepts early on, and my attempts to make the clear will then seem to
you to be a tedious, and even patronizing exercise in belaboring the
obvious. In that case, please bear with me. I'll get to something
interesting eventually. On the other hand, if some of the material
drives you crazy - especially where I ask you to work out
brain-bursting things for yourself - remember that the rest of the
course will be much less weird than this chapter,
and I'm only going to expect you to master the basics
of this deductive logic stuff.
Deductive Arguments
If you already "know" a simple
definition of the difference between deductive and inductive arguments,
you should read the following definitions very, very, very carefully.
The simple definition that I have in mind is very, very easy to
remember. It is also absolutely wrong, and the person who told it to
you knew absolutely nothing about deductive logic. I'm not kidding.
There is a totally dumb definition out there, and irresponsible people
are misleading their students by teaching them this dumb, dumb, dumb,
dumb, dumb, dumb, dumb, dumb, dumb, definition.
(So if you have never heard the simple "definition," you already know
more than the people who have!)
Here is the correct definition. Arguments come in two flavors.
There are deductive arguments, which
establish the precise logical relationships between ideas, and there
are inductive arguments which establish
truths about the universe we live in. Deductive arguments can give you
certainty, but that certainty only applies to the logical relationships
involved. Inductive arguments can prove things about the
world, but the price of never giving you absolute certainty.
Another way to express the difference between the two kinds of
arguments is to say that deductive arguments with true premises either
succeed completely or they fail absolutely, whereas inductive arguments
only have degrees of success. Even the best inductive argument with
absolutely true premises still allows a logical possibility that its
conclusion is false. Even the worst inductive argument with absolutely
true premises still give some logical support to
its conclusion, as pathetically inadequate as that support may be.
Confused? Dismayed? Disturbed? Good! If these definitions
sound weird to you, that's a sign you're beginning to understand them.
Inference
An inference is sort of a basic
minimum-size argument. Arguments, as you will see, can get very big and
complicated, and can contain lots of little argument-bits that are
supposed to fit together to make one big argument for the main
conclusion. Think about it this way. In the previous chapter we spent a
little time breaking big arguments down to smaller ones. Imagine that
we had broken all our arguments down into the smallest sub-arguments we
possibly could. In that case, each smallest possible sub-argument would
then represent a single inference. Now, big argument can contain a
mixture of deductive and inductive inferences,
each of which may have to be evaluated seperately in order to tell
whether or not the big argument works as a whole.
The way to think about the difference between deductive and
inductive inferences is like this. Assume we have a set of two claims,
claim A and claim B. Now suppose someone says that if claims A and B
are both true, then together they would make it absolutely
certain that some third claim, claim C, is true. If this person is
right that A and B together would make C certainly true, then there is
a "valid" deductive inference from A and B taken
together to C. If, however, A and B together don't make
C certainly true, then there is no
valid deductive inference from A and B to C.
Even if we cannot make a deductive infrence from A and B to C,
we might still be able to make a "strong" inductive
inference from A and B to C. This is because it still might be true
that A and B together would make it very likely
that C is true. If it is the case that A and B, if both true, would
make C very likely to be true, then there is a strong inductive
inference from A and B to C.
Notice that a good deductive inference is called "valid,"
while a good inductive inference is called "strong." This is to avoid
confusion in those cases where there's a good inductive,
but no good deductive inference from some set of
facts to a conclusion. Using the word "strong" makes it clear that
you're not claiming that there's a good deductive
inference.
To tell whether an argument is deductive or inductive, you
ignore the question of how the premises are established, and whether or
not they are true or false, and focus on the logical form of the
argument as it is presented to you. Here is a deductive
argument.
All cats are selfish.
Socrates is a cat.
Socrates is selfish.
Assuming that there's nothing wrong with the logical form of
this argument, and that the premises are true, it follows that the
conclusion is absolutely true. Think about it. If it is true that
Socrates is a cat, and that all cats are selfish, could it possibly be
true that Socrates is not selfish? Now here's an inductive
argument.
All cats known to
history are selfish.
All cats are selfish.
Again assuming that there's nothing wrong with the logical
form of this argument, and that the premise is true, it follows that
the conclusion is very very likely, but it does not follow that the
conclusion is absolutely true. Think about it. If
every cat everyone has ever known has been selfish, then wouldn't you
strongly tend to think that all cats are selfish? But could you be
absolutely sure that there wasn't some cat, unknown to history, that
was not selfish?
The forms of these two particular arguments have special
names. The form of the deductive one is called a categorical
syllogism and the inductive one is called a statistical
syllogism. Here's those forms expressed symbolically in
a way that highlights their most essential difference.
All X are Y
Z is X
Z is Y (Categorical syllogism)
A very high proportion of X
are Y
Z is X
Z is Y (Statistical syllogism)
The difference here is subtle, but it's important. Notice that
the first argument deals exclusively in black-and-white concepts. It
says flatly that all X are Y, and admits of no
exceptions. In fact, you could say it basically defines
X as a kind of Y, or that it subsumes the idea of X under the idea of
Y. In any case, it deals in certainty. The second argument, however doesn't
define X as a kind of Y, or subsume the concept of X under Y. Instead,
it allows for the possibility that some X isn't
Y. This means that even if its premises have been proved with 100%
certainty, its conclusion is still only probably
true.
Here's an example of each kind:
All politicians are corrupt
Melvin is a
politician
Melvin is corrupt (Categorical syllogism)
Politicians strongly tend to
be corrupt
Melvin is a
politician
Melvin is corrupt (Statistical syllogism)
Inductive arguments also have logical forms. (Because their
premises are also logically related to their conclusions.) Compare the
form of a categorical syllogism with a statistical
syllogism. Oh, and don't be fooled by the names! Here,
the word "categorical" means something like "makes a claim about all
of something" and "statistical" means "makes a claim about most
of something."
Categorical Syllogism (Deductive)
1. All
badgers are anarco-syndicalists.
2. Hiram is a badger.
C. Hiram is an anarco-syndicalist.
Statistical Syllogism (Inductive)
1.
Almost all badgers are anarco-syndicalists.
2. Hiram is a badger.
C. Hiram is an anarco-syndicalist.
Notice how the addition of the word "almost" transforms a
deductive argument into an inductive argument? This is because that
addition transforms it from an argument where, if the premises are
true, the conclusion is certainly true, to an
argument where, if the premises are true, the conclusion is very
probably true. That's the essential
difference between deductive and inductive arguments, the logical
relationship between premises and conclusion. In deductive
arguments that relationship is either hard and fast, or it is
nonexistant. In inductive arguments that relationship can get pretty
damn firm, but it never approaches the adamantine hardness possible in
deductive arguments. This creates a fundemental difference in how
deductive and inductive arguments can be handled. Because every
certainty is always exactly equal to every other certainty (you're
always 100% sure, no matter what it is you're certain about), and
because deductive arguments that fail always fail totally, every
deductive argument of any given form is always exactly as valid or
invalid as every other argument of that same deductive form. This means
that there is a fundemental difference between validity and cogency.
All valid arguments are equally valid, but all cogent arguments are not
equally cogent. Instead, there are degrees of
cogency, in which we can judge that one inductive argument is more
cogent than another. So while the way deductive arguments differ from
each other allows us to name the deductive forms
in such a way that valid forms will always have different names from
invalid forms, it is not at all practical to name the inductive
forms in a way that allows is to distinguish the cogent from the
incogent by name. For instance, the categorical syllogism is a valid
deductive form, so all categorical syllogisms are
valid arguments. To say that some argument is a categorical syllogism
is thus to say that it's valid. Not so with statistical syllogisms.
1.
99.9% of badgers are anarco-syndicalists.
2. Hiram is a badger.
C. Hiram is an anarco-syndicalist.
1. 99%
of badgers are anarco-syndicalists.
2. Hiram is a badger.
C. Hiram is an anarco-syndicalist.
1. 90%
of badgers are anarco-syndicalists.
2. Hiram is a badger.
C. Hiram is an anarco-syndicalist.
1. 75%
of badgers are anarco-syndicalists.
2. Hiram is a badger.
C. Hiram is an anarco-syndicalist.
1. 50%
of badgers are anarco-syndicalists.
2. Hiram is a badger.
C. Hiram is an anarco-syndicalist.
1. 10%
of badgers are anarco-syndicalists.
2. Hiram is a badger.
C. Hiram is an anarco-syndicalist.
Notice how the arguments starts off pretty darn strong, but
get weaker and weaker as the percentage shrinks.
Notice that, if
its premises are true, the categorical
syllogism can prove its conclusion with certainty, which is what makes
it a deductive argument, while the statistical
syllogism can only ever prover its conclusion with a very high
probability, which is what makes it an inducive argument.
Here are some more examples of deductive
arguments.
|
No fallacy is a
logically compelling argument. Your argument is a fallacy, so it's not
a logically compelling argument.
|
Sam is either a monkey
or a supermodel. He's not a supermodel, so he's a monkey
|
Cheese is a mineral, and
cheese is not a mineral, so cheese both is and is not a mineral
|
Ralph sells onions and
Ralph is French, so Ralph sells onions.
|
|
All monkeys are
primates. George is a monkey, so it follows that George is also a
primate
|
All monkeys are
primates. Pam is a primate, so it follows that Pam is also a monkey.
|
All monkeys are
primates. Nick is not a monkey, so it follows that Nick is not a
primate.
|
All monkeys are
primates. Oswald is not a primate, so Oswald is not a monkey
|
|
Dogs are cats, and dogs
are not cats, so Elvis is alive!
|
Monkeys are made of
cheese, and Elvis was a robot, so dogs are or are not cats.
|
Elvis is not dead, so
Elvis is alive.
|
All monkeys are
primates, so all primates are monkeys.
|
And for contrast, here are some examples of inductive
arguments.
|
George looks exactly
like Norm, who is a primate, so George is also a primate
|
Pam is a primate, and
many primates are monkeys, so it Pam is also a monkey.
|
Analysis of 30,000
wheels of cheese revealed no mineral content, so cheese is not a
mineral
|
I saw Ralph give someone
some onions in exchange for money so Ralph sells onions.
|
|
Most arguments of that
type fail, so your argument must fail too.
|
Sam is very hairy and
has hands and a prehensile tail, so he's a monkey
|
George says Nick is not
a primate, so Nick is not a primate.
|
Everyone who ate the
fish died, so the poison was in the fish
|
|
All Frenchmen eat
snails, so everyone in the world eats snails.
|
Lots of smokers get
cancer, so smoking causes cancer.
|
Elvis was dead last time
anyone checked, so Elvis is not alive.
|
No-one has ever seen a
hippogriff, so they don't exist.
|
Proving Stuff
Can a deductive argument prove something about the
world with absolute certainty? No. No argument is ever
stronger than its weakest premise. If a deductive argument has a
conclusion that's about the world, then it must have a premise that is
also about the world. Ultimately, that premise must be justified by
observation, by looking at the world. All arguments based upon looking
at the world are inductive arguments, so every conclusion about the
world, whether it shows up in an inductive or a deductive argument, is
ultimately based on some inductive argument. The bottom line is that
nothing apart from logical relationships between ideas can be known
with certainty. Conclusions about the world always come with at least
some uncertainty.
Another way to look at the difference between inductive
arguments and deductive arguments is to say that in an inductive
argument it is assumed that the premises, if true, make the conclusion very
likely to be true. Whereas in a deductive argument is assumed
that the premises, if true, make it impossible for the
conclusion to be false. To put it another way, an inductive
argument attempts to show that its conclusion is very probably
true while a deductive argument attempts to show that its conclusion is
certainly true. (Confused? Don't worry about it. If
you don't see how the distinction beween "probably" and "certainly"
applies here, you're not alone. Most people find this the
hardest part of logic to get - I've even met a professor who doesn't
understand it - and it won't be on the test.)
This distinction does have one useful consequence. If the
argument you are dealing with is deductive, and
you can show that it is possible for its
premises to be true when its conclusion is false,
then you will have shown that it is a bad argument. (Technically, this
is called showing that it has an invalid form.) In terms of the SCAEFOD
procedure, it follows that once you have figured out that an argument
does not rely on analogy, or an authority, and does not make a
generalization, or support a causal claim, or claim that its conclusion
explains something else, or depend on burden of proof, then all
you have to do to refute the argument is to show that its
premises can be true even if its conclusion is false. If a
deductive argument's conclusion can be false,
even if its premises are true, then it's simply
not a good arguement.
(The study of relationships between ideas is called formal
logic or, (because it's easier to do with symbols), symbolic logic. In
order to get more than a basic handle on symbolic logic, it's necessary
to learn the language. We're only going to do the basics here, so no
language lesson. (Yay!) )
Deductive Concepts
Before I get into the business of evaluating deductive
arguments, I want to try to ease you into the subject by covering a few
important concepts.
All-or-Nothing Statements
An "all-or-nothing" claim is the kind of claim that can be
proved false by even a single counter example.
"All Scots eat haggis" is this kind of claim because if there exists
even one Scot who does not eat haggis, the claim is false.
All-or-nothing claims overwhelmingly tend to be false
in real life, but they are the only kind of claim
that deductive logic can deal with, which is one of the things that
makes deductive logic seem pointless to many people.
Necessary and Sufficient
Conditions
Necessary and Sufficient Conditions
(Inductive)
When you talk inductive, you talk about what people actually
experience out there in the world, so here we should use physical
examples.
Say in room number one you have a loose pile of really
dry kindling that's cut really thin, and which includes copious amounts
of very delicate wood shavings. And also say that all this is resting
on a really hot metal surface, say 270 degrees
Celsius in an airtight room that has no atmosphere
whatsoever. What's going to happen? It won't be a fire
because, without oxygen (or another oxidizing substance), there cannot
be combustion. Another way to put this is to say that the presence of
an oxidizer is a necessary condition for
something to catch fire.
Suppose we have another room with an oxygen atmosphere and a
red-hot floor, but there's no kindling or any other kind of fuel in the
room. Again no fire, because a fire requires fuel, and there's none
here. From this it follows that the presence of fuel is also
a necessary condition for a fire to
happen.
You can also think about a room with plenty of air and
kindling, but a stone cold floor. Will a fire start without a heat
source? No, so a heat source is also a necessary
condition for a fire.
We can also run this the other way. Is fuel, all by itself,
enough to make a fire? No it isn't, so while fuel is
a necessary condition for a fire, it is not a sufficient
condition for
a fire. The same can also be said for oxidizer and ignition-temperature
heat source. None of these, by itself, is sufficient
to make a fire.
Now consider a suspension bridge over a rocky gorge. How many
different conditions can you think of that would be sufficient
to bring this bridge down? I can think of several. For instance, a
five-kiloton nuclear explosion should do nicely. Of course, it doesn't
have to be a nuclear explosion. Five tons of TNT
set off in the middle of the bridge should also do the trick. There's
also meterorites. A one-ton meterorite hitting the bridge would not
only take down the bridge, it would also vaporize it, and the rocky
gorge as well, and most of the nearby mountains too. (Be cool to watch,
too.) Finally, imagine if a convoy of trucks carrying liquid nitrogen
all spilled their loads at once and supercooled a large number of the
suspension cables, making them too brittle to take the load, that would
take down the bridge too. Or if we magically changed the roadbed to
Wenslydale cheese and the cables to Mozzarella. Notice that any
one of these conditions is sufficient to take out
the bridge, even though none of them is necessary
to take the bridge down. Nuclear weapons are not necessary because we
could take the bridge down with conventional explosives, conventional
explosive are not necessary because we could take the bridge down with
a nuke, or cheese magic, or . . .
Is it always easy to specify necessary and sufficient
conditions? Well, when we're dealing with causal relationships in the
real world, it can often be really difficult to say what's necessary or
what's sufficient to bring about a particular effect. In the
looking-glass world of deductive logic, things can be a lot easier.
Necessary and Sufficient Conditions
(Deductive)
By definition, a "bachelor" is a man of marriagable age who
has not yet married.
Jimmy is male, unmarried since birth, and 14 years old. Is
Jimmy a bachelor?
Jane is female, unmarried since birth, and 24 years old. Is
Jane a bachelor?
Joe is male, married three seconds ago, and 24 years old. Is
Joe a bachelor?
If you said "yes" to any of those questions, go back and look
at the definition again. Jimmy is not of marriagable age, and so he
lacks that necessary condition to be a bachelor. Jane is not male, and
so she lacks that necessary condition to be a
bachelor. Joe is not unmarried, and so he lacks that
necessary condition to be a bachelor.
How about Absalom, who is a male human who has never been
married and is now 86 years old? Well, by the definition given above,
Absalom is a bachelor! The conditions of being a man, being old enough
to marry, and having never married are jointly sufficient
to make Absaom, or anyone else, a bachelor.
- By definition, an "Aylesbury duck" is a large domesticated
duck with pure white plumage, a pink bill and orange legs and feet.
- By definition, a "Mandarin Duck" is a medium-sized with a
red bill, a white crescent above the eye and reddish face and
"whiskers".
- By definition, a "Ringed Teal" is a small duck with a
chestnut back, pale grey flanks and a salmon-coloured breast speckled
in black.
- By definition, an "Abacot Ranger" is a duck with a 'hood'
of fawn-buff feathers and a creamy white body streaked with colour.
- By definition, a "Red-crested Pochard" is a large diving
duck with a rounded orange head, red bill and black breast.
- By definition, an "Indian Runner" is a domestic duck that
stands erect like a penguin and runs rather than waddling.
Being an Abacot Ranger is sufficient for
being a duck, because you can't be an Abacot
Ranger without also being a duck.
But being an Abacot Ranger is not necessary for
being a duck, because you can be a duck without
also being an Abacot Ranger.
Notice that the deductive necessary and
sufficient conditions are abslolutely cut and dried. Once we've
established that Jimmy, Jane and Joe all lack one of the necessary
conditions, we've established for certain
that none of them is a bachelor, Once we've established that Absalom
meets all three necessary conditions, we've
established for certain that he is a
bachelor, Things are not quite so certain back in the inductive
realm. While I can't begin to think of any way to make fire without
fuel, without oxidant or without heat, I can't absolutely guarantee
that there isn't one, so I can't absolutely guarantee
that these conditions are absolutely necessary for fire.
Remember:
For a statement to be a lie, it is necessary for it to be untrue,
but merely being untrue is not sufficient to make it a lie, because it
might have been an honest mistake.
Sticking a lit road
flare into a loose pile of dry kindling is sufficient to set it ablaze,
but a road flare is not necessary to start the fire, because a powerful
laser or some burning gasoline would do just as well to start a fire.
Stipulation
We don't bother to prove the premises of deductive arguments.
Basically, we just stipulate that they're true. We assume them, and
then go on to look at the logical relationship
between those premises and the conclusion. Deductive logic is
all about logical relationships. It doesn't, by itself, try to prove
things about the world. Instead, it investigates logical relationships
between definitions and othere stipulative statements.
Conditionality
A "conditional" claim is one that says that if
one thing is true, then another thing is true.
The following are all conditional claims.
If wishes were horses, then beggars would ride.
If cats wore hats, then dogs would wear clogs.
If Hawk the Kitty wore a hat, then Patch the Dog would wear clogs.
Notice that these statements don't have to make sense, and
we're really not interested in whether they're true or not. All we care
about in deductive logic is their relationship with other claims.
Seriously, conditional statements don't have to make sense. Here's some
perfectly good (for our purposes) conditional statements.
If Al Gore was president, then Marie Antoinette was actually a
three-legged alien death machine controlled by a crew of 247 white mice.
If trees eat bees then you can live on the knees of cheese
If Joe is a Jumbuck then Bob is a Billabong.
But notice that these statements only run one way. saying that
"if Joe is a Jumbuck then Bob is a Billabong" does not
imply that "if Bob is a Billabong then Joe is a Jumbuck," oh dear me
no! If we happen to find out that Bob is in fact a Billabong, that
tells us nothing about whether or not Joe is a
Jumbuck!
Necessary and Sufficient Conditions Redux
Now, it's important to notice that conditional statements are not
causal statements."If Joe is a Jumbuck then Bob is
a Billabong" does not mean "If Joe becomes
a Jumbuck then Bob will become a Billabong." What
it means is that, if you check on Joe, and he turns out to be a
Jumbuck, then it follows that Bob has been a Billabong all along.
Nothing causes anything to change.
Instead, conditional statements can be thought of as setting out
deductive necessary and sufficient conditions for related claims.
For instance, the statement "If Joe is a Jumbuck then Bob is a
Billabong" sets out two conditions.
First, it says that Joe being a Jumbuck is sufficient
for Bob to be a Billabong
Second, it says that Bob being a Billabong is necessary for
Joe to be a Jumbuck.
Think about it.
Now think about whether it says that Joe being a Jumbuck is necessary
for Bob to be a Billabong, or whether it says that Bob being
a Billabong is sufficient for Joe to be a
Jumbuck.(Hint: It doesn't.)
When you're done with that, think about the logical status of
statements like "all coneys are lapins." How is it related to
conditional statements?
Well, think about this:
Does it say that being a coney is a sufficient condition
for being a lapin?
Does it say that being a coney is a necessary
condition for being a lapin?
Does it say that being a lapin is a sufficient condition
for being a coney?
Does it say that being a lapin is a necessary
condition for being a coney?
(Answers yes, no, no, yes.)
So, in essence, "all coneys are lapins" says both "being a
coney is a sufficient condition for being a
lapin" and "being a lapin is a necessary condition
for being a coney." Now, where have we seen that form before? Well,
we've seen it before in "if _____ then _____ " statements, otherwise
known as conditional statements, so "all
coneys are lapins" can be rewritten as "if somthing is a coney, then
that thing is also a lapin."
Notice again that "all ____ are ____ " statements are no more
reversable than "if ____ then ____ " statements. Just because all
housecats are felines it doesn't follow that all felines are housecats.
Reciprocity
Finally, notice that the relationship of necessity
is reciprocal to the relationship of sufficiency.
If A is necessary for B, then it follows that B
is sufficient for A, and vice versa. In fact,
they're basically the same relationship, seen two different ways.
For example, if being a coney really is a necessary
condition for being a lapin, then it will follow that being a lapin is
a sufficient condition for being a coney. And if
being a coney really is a sufficientcondition for
being a lapin, then it will follow that being a lapin is a
necessary condition for being a coney.
Evaluating Deductive Arguments
Although I'm having you treat every argument you can't
otherwise identify as a deductive argument, "deductive" arguments are
actually a very specific kind of argument, precisely defined and
beloved by logic geeks everywhere. So, if you'll forgive a little bit
of geekery, here's the skinny on deductive arguments.
A deductive argument is one that relies on the purported truth of its
premises and on the purported fact that it is
impossible for those premises to be true if the conclusion is false.
(Any argument that isn't "deductive" is "inductive.")
A deductive argument that has good logical form is called "valid,"
one that doesn't is called "invalid."
Invalid deductive arguments are no good. Pshaw! They're crap. (And they
know it, the stinkers.) By the way, this is something that only
applies to arguments. Only arguments can be valid
or invalid. Statements can be true or false, but
they can't be valid or invalid.
A valid deductive argument with true
premises is called "sound." A sound
argument has a true conclusion. Period.
If it's sound, its conclusion is true. Not, "most
likely," not "really really probable." Just plain flat true! (Of
course, for this to work we have to be absolutely sure those premises
are true.)
Validity: The Easy Part
Before I get into the easy part of
validity, I'm just going to mention, but not test you on yet, the real,
correct and true definition of "validity". Here it is: (Accept no
substitutes.)
An argument is valid if, and only if
it is impossible for there to be a situation in
which all its premises are TRUE and its conclusion
is FALSE.
Scared? Confused? I don't blame you. Many, many, many people
have a very hard time understanding this definition, so I'm reserving
the hard bits for the next chapter. This means
you don't have to deal with the full definition of validity until then.
For now, I'm giving you a simplified rule for validity to get you
through this chapter
The Easy Implication of Validity
The correct definition has three logical implications. Two of
those implications are weird and hard to understand, but one is pretty
straightforward, so we'll deal with the easy implication first and
leave the other two for the next chapter.
Easy Implication: If the argument is such that
its premises, if true, logically force the conclusion to be true, then
the argument is valid.
You could also say this as "an argument is valid if the
premises make the conclusion true" or "if you can't
make the conclusion false without also
making at least one premise false, then the
argument is valid" or "if the premises, taken all together, force the
conclusion to be true, the argument is valid."
Now I want to point out an Important and Ansolutely True Fact.
The following statements are all FALSE
- If an argument is valid,
then the argument is such that its premises, if true, logically force
the conclusion to be true. (False!)
- If an argument is valid,
the premises make the conclusion true. (False!)
- If an argument is valid,
you can't make the conclusion false without also
making at least one premise false. (False!)
- If an argument is valid,
the premises, taken all together, force the conclusion to be true. (False!)
This is because the premises making the conclusion true is a sufficient
condition for the argument to be valid, but is absolutely not a necessary
condition for the argument to be valid. We will talk about the other
ducks, I mean the other ways of making an argument valid in the next
chapter.
How to Think About Validity
The correct way to think about this is to think about assumptions
and possibilities. When you look at one
of the arguments given in this chapter say to yourself, "now, if I assume
that all these premises are true, is it possible
for this conclusion to be false?" (This
test works for all the arguments in this chapter. Other kinds of valid
arguments will be dealt with later)
The definition I'm giving here is sufficient
for an argument to be valid. But it's only one of the ways an argument
can be valid, so it's not a necessary condition
for an argument to be valid.
When checking arguments for validity, assume that all the
premises are true, then ask yourself if it is now
possible for the conclusion to be false. If the
answer is "yes," the argument is invalid (wonky).
If it's "no," the argument is valid. (No, I
didn't get it mixed up. That's the rule.)
Now possible for conclusion to be false = invalid
(wonky)
Now impossible for conclusion to be
false = Valid
For instance, the following arguments are all completely invalid
(wonky).
Paris
is in France
Berlin is in Germany
Compton is in America |
Cats
are mammals
Dogs are mammals
Ferrets are mammals |
People
have two legs
Mammals have four legs
Insects have six legs |
Dumbledore
is a wizard
Gandalf is a wizard
Merlin is a wizard |
Example 1
If George Washington had been poisoned, shot, beheaded and
then burned to ashes by his wife for his constant adultery, he would
now be dead. George was not poisoned, shot, beheaded and then burned to
ashes by Martha (pity), so he's not dead.
1. If Martha Washington
had gone absolutely postal on George's ass, he would be dead.
2. Martha was strictly non-postal.
C. George ain't dead.
If these premises were true, would it be possible for the
conclusion to be false. Absolutely! George could have died from some
other cause, say a bad cold caught when avoiding the irate father of a
young woman he had seduced, so it's logically possible for the sentence
"George ain't dead" to be false, even if we assume the truth
of the premises. So it's invalid (wonky).
Example 2
If carnivorous faerie-pixies had sprinkled their magic
barbeque sauce on Ghengis Khan, ol' Ghengis would now be a used car
salesman working out of Bakersfield with an unhappy wife, two
overweight children and a suspicious rash. Well, carnivorous
faerie-pixies did sprinkle magic barbeque sauce on ol' Ghengis, so
Ghengis Khan has a rash and so on.
1. If
pixies had BBQ sauced Ghengis Khan, Ghengis would be a rash-infested
used car salesman working out of Bakersfield.
2. Pixies did BBQ sauce Ghengis Khan.
C. Ghengis does have a rash.
Now, to check validity, we suspend
disbelief on the premises and assume that they're
true. So if we assume magic
barbecue sauce exists and will have these effects
when sprinkled, then Ghengis Khan will be in
Bakersfield and so on. One of the effects of the sauce is a suspicious
rash so, given the truth of the premises, the
statement "Ghengis Khan has a rash" can't be
false. So this argument is valid. That's
right, VALID!
Example 3
You know that big black and white swimming thing they have
down at Seaworld, They call it "Shamu," and it's either a cat or a dog.
Well, it's certainly not a dog, so it must be a cat.
Shamu
is either a cat or a dog
Shamu is not a dog
Shamu is a cat.
Remember again that validity has nothing to do with whether or
not the premises are true. What it depends on whether the conclusion could
be false, if, the premises were
true. Now, if these premises were true, could the
conclusion be false? It couldn't, so this argument is valid.
Now check these arguments for validity. (Figure out which are
valid and which aren't before you look for the answers.)
1. All
monkeys are primates. George is a monkey, so it follows that George is
also a primate.
2. All
monkeys are primates. Pam is a primate, so it follows that Pam is also
a monkey.
3. All
monkeys are primates. Nick is not a monkey, so it follows that Nick is
not a primate.
4. All
monkeys are primates. Oswald is not a primate, so Oswald is not a
monkey.
Answers: 1. valid, 2. invalid, 3. invalid, 4. valid.
Remember, the actual truth or falsity of the
premises is irrelevant, completely irrelevant,
to the validity of the
argument. Validity is just about the logical relationship
between the parts of the argument, nothing else.
Logical Form and Validity
Now, some deductive logical forms are so common,
and so important, that they get their own names. Here's five of them.
Modus Ponens
If
X is true, then Y is true.
If Babe is
a shoat, then Joe is a Mocklin
If Roy is a
tramp, then Roy is a bum
X is true
Babe
is a shoat
Roy
is a
tramp
Y is
true Joe
is a
Mocklin Roy
is a bum
Affirming the Consequent
If
X is true, then Y is true.
If Babe is a shoat,
then Joe is a Mocklin
If
Roy is a tramp, then Roy is a bum
Y is true
Joe
is a
Mocklin
Roy
is a
bum
X is
true
Babe is a
shoat Roy
is a tramp
Denying the Antecedent
If
X is true, then Y is true. If
Babe is a shoat, then Joe is a Mocklin
If
Roy is a tramp, then Roy is a bum
X is not true
Babe
is not a
shoat Roy
is not a
tramp
Y is not
true
Joe is not a
Mocklin Roy
is not a bum
Modus Tollens
If
X is true, then Y is true. If Babe is a
shoat, then Joe is a Mocklin
If Roy is a
tramp, then Roy is a bum
Y is not true
Joe
is not a
Mocklin Roy
is not a
bum
X is not
true Babe
is not a
shoat
Roy is not a
tramp
Disjunctive Syllogism
Either X is true or Y is true.
Either Babe is a shoat or Joe is a
Mocklin Roy is either a bum or a tramp
Y is not true
Joe
is not a
Mocklin Roy
is not a
bum
X is
true
Babe is a
shoat
Roy
is a
tramp
In each of the above groups, the first argument is
the general statement of the form, the second is a specific instance of
the form, and the third argument is an instance of a special case of
the form that is easier to deal with in pictures.
Which ones are valid? Which ones are not? Well, to
figure that out for the first four, you have to make sure that you
understand that "if Babe is a shoat, then Joe is a Mocklin" just
means that "if Babe is a shoat, then Joe is a Mocklin." It does not
go on and say "if Joe is a Mocklin, then Babe is a shoat." That
particular claim is not a part of any
of these arguments. Because the second claim is not
made or implied by "if Babe is a shoat, then Joe is a Mocklin," the only
way "if Babe is a shoat, then Joe is a Mocklin," can be false
is if Babe is a shoat but Joe is not
a Mocklin. (This is because it's an "if-then" statement.) It doesn't
say that Babe is a shoat, and it doesn't
say that Joe is a Mocklin. It just says that if
Babe is a shoat, then Joe is a Mocklin.
Too complicated? Well, then we'll go with an
easier example. I've got these special case Roy tramp/Roy bum arguments
which can be easily done in pictures, and which
will hopefully make the difference clear. As before, the only
way that "if Roy is a tramp, then Roy is a bum" can be false is if Roy is
a tramp, and Roy is not a bum. Under all other
circumstances that statement will be true. Here's
the same point in pictures. Only one of the
following pictures makes "if Roy is a tramp, then Roy is a bum" false.
All the other pictures make it true.
Picture 1
Picture 2
Picture 3
Picture 4
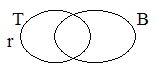
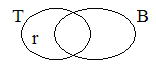
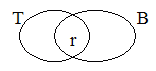
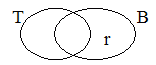
Roy is neither a tramp nor a bum.
Roy is a tramp but not a bum.
Roy
is a tramp and a bum.
Roy is not a tramp
but is a bum.
Well, notice that in picture 2 Roy is a tramp but
is not a bum. That couldn't be true if "if Roy is
a tramp, then Roy is a bum" was true, so picture 2 makes "if Roy is a
tramp, then Roy is a bum" false. All of the
other pictures are logically compatible with "if Roy is a tramp, then
Roy is a bum" because they could be true even if "if Roy is a tramp,
then Roy is a bum" was true. So none of the
other pictures makes "if Roy is a tramp, then Roy is a bum" false.
Now, there's an easier way to convey this
information with pictures. We can draw a picture in which putting the
"r" in the "T" circle means also putting it in
the "B" circle. This is easy, because all we have to do is draw the T
circle inside the B circle. Like so:
Picture 5
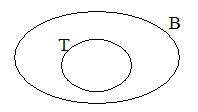
(This actually says "all tramps are bums," which
is a little stronger than "if Roy is a tramp, then Roy is a bum," but
I'm not going to worry about that here.)
Now copy out the above picture four times, and
take each of the conditional-based forms (Modus Ponens, Affirming the
Consequent, Modus Ponens, Denying the Antecedent) in turn, and try to
draw in an "r" to make the premises of that form true,
and the conclusion false. (Picture five, as it
stands, already makes the first premise of each form true. You just
have to make the conclusion false while leaving the second premise
true.) Look beside the name of each form below to check your answer.
Modus
Ponens
Affirming the Consequent
If Roy is a
tramp, then Roy is a
bum If
Roy is a tramp, then Roy is a bum
Roy is a
tramp Roy
is a
bum
Roy is a
bum Roy
is a tramp
Denying the Antecedent
Modus
Tollens
If Roy is a
tramp, then Roy is a bum
If
Roy is a tramp, then Roy is a bum
Roy is
not a
tramp Roy
is not a
bum
Roy is not a
bum Roy
is not a tramp
Answers, modus ponens and modus tollens are valid,
affirming the consequent and denying the antecedent are invalid.
Okay, so now you've figured out that affirming
the consequent and denying the antecedent
are invalid. (They are actually our first two deductive fallacies,
because they are argument forms that look sort of like good forms, but
which are really terrible.) The most interesting one is the valid
form modus tollens, which is one that
many people don't expect to be valid. (And lots of people take a while
to figure out why it's valid.) Nevertheless, it's
an important and interesting form, especially since it gives us one of
our ways of proving a negative statement.
Think about it, if we can prove that if Roy was a
tramp, then he would be a bum, and we could also
prove that Roy isn't a bum, then that's enough to
prove that Roy isn't a tramp either. If it's true that if Roy was a
tramp, then he would be a bum, is is it possible for him to be a tramp without
also being a bum? No it isn't, so the fact of his not being a bum would
then prove adsolutely that he was not a tramp.
More on Disjunctive Syllogism
We've seen the fallacy of "false choice," where an
arguer illegitimately claims that the number of possibilities is less
than it really is. But what about real choices?
What about when there really are only two
possibities? If that is really the case, and
you can eliminate one of the only two possibities, well then you can
apply the valid argument form of
"disjunctive syllogism" and get a sound argument.
1. George is
either alive or dead.
2. George isn't dead.
C. George is alive.
Now here's the tricky bit. The paragraph above
leaves out one little detail. We have to be careful not to confuse the
concepts of fallacy and validity.
False Choice isn't a fallacy because of invalidity. It's actually a
perfectly valid disjunctive syllogism in form.
The only thing that makes false choice a fallacy is that the crucial
premise, the one that limits our choices, is false.
Look at the following argument.
1.
Shamu is either a cat or a dog
2. Shamu is not a dog
C. Shamu is a cat.
Notice now that both arguments have the same valid form. The
second argument only fails because the first
premise is false. Dog and cat are not the only two possibilities for
Shamu's species. Now let's look at disjunctive syllogism through
pictures and the following argument.
Roy is
either a bum or a tramp
Roy is not a
bum
Roy is a tramp
Now, it's important to know that in logic, the word "or" is
always taken to mean that it could be one and it also
could be the other. You are not
supposed to add the "and not both" that many people mentally add when
they say "or." In logic, "or" should alsways be understood as
saying, "one or the other, or both." The following three pictures
therefore all make "Roy is either a bum or a
tramp" true.
Picture 2
Picture 3
Picture 4
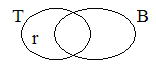
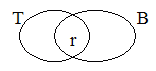
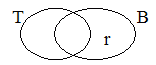
Roy is a tramp but not a bum.
Roy
is a tramp and a bum.
Roy is not a tramp
but is a bum.
If Roy is a tramp but not a bum, then the statement "Roy is
either a bum or a tramp" is true.
If Roy is a tramp and a bum, then the statement "Roy is either a bum or
a tramp" is true.
And if Roy is not a tramp but is a bum, then the statement "Roy is
either a bum or a tramp" is true..
Now, out of those three pictures above, which one also
makes the statement "Roy is not a bum" true? It's picture 2, isn't it?
Picture 2
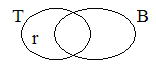
Roy is a tramp but not a bum.
Now, this is the only picture that makes both
of the premises true.Does it make the conclusion
true? If it does, the argument form is valid.
Terminology Reminder
Remember, a logically good deductive
argument is called valid, and a valid argument
with true premises is called sound. A
logically good inductive argument is called strong,
and a strong argument with true premises is called cogent.
The words "valid" and "sound" are not used for inductive
arguments, and the words "strong" and "cogent" are not
used for deductive arguments.
Copyright © 2012 by Martin C. Young
This
Site is Proudly Hosted By.