Arguments, and Sampling Arguments

This chapter will discuss the following topics:

What arguments are.
The nine argument strategies.
The sampling argument strategy.
The main three issues in sampling arguments.
The main logical fallacies associated with sampling arguments.
Argument tactics.
How to analyze and evaluate a dispute involving two or more opposing arguments.

After studying this chapter, you should be able to:

Tell the difference between arguments and claims.
Identify argument strategies in the most obvious and easy cases.
Tell the difference between sampling and non-sampling arguments in most cases.
Know generally what to think about when considering the age of a sample.
Know generally what to think about when considering the size of a sample.
Know generally what to think about when considering the method by which a sample was chosen.
Identify samling-related fallacies in obvious cases.

Sampling
Correlation
Authority
Burden of proof
Explanation
Physical Analogy
Logical Analogy
Deductive

For the purposes of this course, the word "argument" will be used to refer to any attempt to persuade another person that some claim is or is not true. This chapter will teach the basic analysis of a special kind of argument I call a "sampling argument." Sampling arguments are commonly used to support general statements. Generalizations are statements that cover the whole of some population, such as Americans, wombats, the water in the oceans, left-handed Armenian mole-diggers, Scotsmen with Irish names, tea-drinkers, trees, people who do horrible things to turnips... well, you get the idea. A sampling argument is an argument that starts with a "sample," a small group of taken by some method from a larger population, and then attempts to persuade us that a feature clearly seen in the sample must therefore also be a feature of the population.

It's important to remember that arguments are categorized by how they attempt to support their conclusions, not by the type of conclusion they have. The conclusion of an argument is a species of claim, and claims are different from the arguments that support them. Here are some claims .

All Spanish soups are served cold.
Composite body aircraft will never be commercially successful.
All heavy metal bands use cellos.
All guitarists are high-ranking academics.
Russian monks are hard to kill.
All televangelists are all hypocrites.

Notice that none of these claims comes with any reason for you to believe it. Each is just a claim. None of them are arguments. Also notice that each of these claims is about all of something. The name for a claim that concerns all of something is "generalization." So these claims are all generalizations.

There are many ways of supporting a generalization, but this chapter is only concerned with one of them. This chapter is about sampling arguments, which have their own peculiar logical structure, their own problems and subtleties, and their own particular ways of going wrong.

Here are some sampling arguments .

I was served gazpacho soup at a Spanish restaurant, and it was ice cold, so all Spanish soups are served cold.
Composite body aircraft will never be commercially successful. Just look at the Beechcraft Starship!
All heavy metal bands use cellos because Apocalyptica is heavy metal, and they use three cellos,
The lead guitarist from Queen is chancellor of a university, proving that all guitarists are high-ranking academics.
Rasputin had to be poisoned, shot, bludgeoned and drowned, so Russian monks are sure hard to kill.
Swaggart and Bakker had affairs, which shows that those televangelists are all hypocrites.

And now, for comparison, here are some arguments that are not sampling arguments.

The Most Interesting Man in the World says that all Spanish soups are served cold. (Sometimes with Dos Equis!)
Composite body aircraft will never be commercially successful, they just cost too much!
All heavy metal bands use cellos because the cello lobby got congress to make cellos mandatory in heavy metal.
Guitar shredding requires graduate work in astrophysics, so all guitarists are high-ranking academics.
Russian monks are routinely equipped with antitoxins, kevlar and snorkels, so they are very hard to kill.
Televangelism is nothing but a pure form of hypocrisy, so all televangelists are hypocrites.

The first thing to notice here is that the arguments in the second group have exactly the same conclusions as the arguments in the first group. These conclusions are all generalizations, but the type of conclusion does not control the type of argument . Arguments are sorted into types according to their "logical strategy", which means the way they go about supporting their conclusions. Arguments in the top group support their conclusions by alluding to a small group (the "sample") taken from a larger, encompassing group (the "population"), claiming that the sample has a certain "feature," and implying that because the sample has the feature, the population must also have the feature. (Arguments in the lower group use a whole bunch of different strategies, none of which we will worry about here.)

Facts, Opinions, Conclusions

Technically, a "fact" is a something that cannot reasonably be disputed, an "opinion" is just something someone believes, and a "conclusion" is something someone thinks other people should believe. In terms of evidence, we can define a "fact" as a claim that is supported by compelling evidence, an "opinion" as a claim that someone thinks is supported by compelling evidence, and a conclusion as a claim that someone says is supported by compelling evidence.

Unfortunately, the words "fact" and "opinion" are occasionally badly misused, as in the following dialog:

Chuvaskaya. So the teacher asked us to analyze this online debate between Doctor Polyp and Professor Spleen. I think Dr. Polyp won the debate because he pointed out that there are no documented cases of people dying as a result of using marijuana, that increases in marijuana consumption have not been followed by increases in disease the way the sharp rise of cigarette smoking was followed by a sharp rise in lung cancer, and that California has more-or-less legalized marijuana without experiencing any noticeable increase in social problems. Professor Spleen doesn't discuss these matters at all, and he gives no evidence to support his claims that marijuana is more dangerous than alcohol and tobacco, and should be illegal. So I think that Doctor Polyp's argument for legalizing marijuana is better than Professor Spleen's argument against it.
Flanders. I disagree. I think your analysis is completely wrong. Look at the debate again. It's true that Doctor Polyp says that noone has died from using marijuana, that marijuana hasn't increased disease, and that California virtually legalizing marijuana hasn't caused any problems, but Professor Spleen has pointed out that marijuana is extremely dangerous and destructive, and it should be absolutely illegal everywhere. So you can clearly see that Professor Spleen has the facts while Doctor Spleen is just giving his own personal opinion.

I want you to carefully examine the above dialog to determine who it is out of Doctor Polyp and Professor Spleen who actually has the facts and who is merely stating personal opinions. Notice that Spleen claims that marijuana is bad and should be illegal, while Polyp disagrees with this, so it follows that they have different conclusions. but the mere fact that two people disagree says nothing about which one of them has the facts. In fact, if all these two did was state opposing opinions, then we would have to say that neither of them had the facts. But also notice that while Spleen says nothing to support his conclusion, Polyp says quite a deal. Polyp gives reasons to believe his conclusion while Spleen does not. In general, if one side of an argument gives reasons and the other side doesn't, the side that doesn't give reasons cannot be said to "have the facts." A side that does not give reasons does not have the facts. Only sides that give reasons can ever be said to have the facts, and, even then those reasons don't always turn out to actually be facts. Furthermore, since Flanders doesn't mention Spleen raising any objections to Polyp's claims, we should assume, based on this dialog, that Spleen has not given us any reason to doubt Polyp's reasons. Thus, if anyone "has the facts" here, it is Polyp who has the facts, and Spleen who is merely giving his personal opinion.

For the purposes of this text, I want you to define a "fact" as a claim that is not actually disputed by anyone. Thus, if one side says that marijuana has never killed anyone, that it does not cause disease, and virtually legalizing it in California hasn't caused problems, and the other side does not dispute these claims, then those claims are the facts in this particular case.

The bottom line is, in this course, you should look to see whether or not a factual claim is disputed by the other side. If the claim is ignored or accepted by the other side, then that claim is a fact, at least as far as this class is concerned.

Recap Questions

Define the following terms from memory and in your own words, and then check your answers against the way these terms are defined in the preceding text. If you can't do that, at least write out definitions of each of these terms in your own words. Make sure you write out these definitions in your own words. If you can't give your own definition of a term, then you don't understand that term.

argument
population
generalization
sample
feature
sampling argument
fact (technical definition)
fact (definition for this course)

When you make your definitions of these terms, try to come up with an example of something that fits each definition. If you have time, you could check and see if your example fits my definition as well as yours.

Sampling

The essence of a sampling argument is the "sample." Usually, populations are so large that we cannot reasonably test the state of every member of that population. For instance, if we wanted to know what proportion of Scotsmen get tipsy (slightly drunk) on Hogmanay, we cannot possibly hire enough obervers to follow around every Scotsman around on the evening of December 31st. (Especially if we count female Scots as "Scotsmen" Oh, lets just call them "Scots."), so we're scre... I mean, so we have to fall back on looking at a much smaller number of Scots and extrapolating the results to all haggis-eatin', kilt-wearin' caber-tossers. (This is perhaps an unfair characterization of the Scots. Very few of them actually toss cabers.) So let's just hire people to follow around a randomly selected group of one million Scots next Hogmanay and to report on whether or not they get tipsy. Say that 75% of these randomly selected Scots get tipsy on Hogmanay, we could then make the following argument.

Exactly 75% of our sample got tipsy this Hogmanay, therefore 75% of all haggis-eaters got tipsy this Hogmanay.

Here's how the terminology of generalization matches up with this argument.

Facts
Population: All Scots (several million of them.)
Sample: One million randomly selected Scots.
Feature being tested: Tipsiness.
State of the sample: 75% tipsy at this Hogmanay.

Conclusion drawn from those facts
State of the population : 75% tipsy at this Hogmanay.

This is how a generalization works, if it works at all. A sample is taken, and it is argued that the state of the sample must be the same as the state of the population. If the state of the sample cannot reasonably be explained without assuming that the population has the same state, the argument is good. If we can reasonably explain the state of the sample without assuming that the population has the same state, the argument is no good, lousy, bogus, wack, heinous.... I'll stop now.

For another example, imagine that two people, call them "Jeeves" and "Wooster," are trying to figure out the overall composition of the following population. Imagine also that neither of them can see the population the way you can. (You can see that this population is extremely well mixed. In fact, there are only two deviations from perfect mixing. They appear in the top left and bottom right corners of the field. By some strange coincidence, that's where Jeeves and wooster take their samples from.) They know that it's composed of 2,600 colored dots, but that's about it. Neither of them has any idea of how the dots are distributed, or anything else besides the fact that it's made up of dots. And of course, neither of them knows that the population is made up of 650 red dots (25%), 650 blue dots (25%) and 1,300 green dots (50%) (You can see that this population is extremely well mixed. In fact, there are only two deviations from perfect mixing. They appear in the top left and bottom right corners of the field. By some strange coincidence, that's where Jeeves and Wooster take their samples from.) Now Jeeves takes a sample from the top left corner of the population (red line) while Wooster takes a sample from the bottom right corner, (blue line). Each of them then makes a claim about the composition of the population based on their samples.

Jeeves's sample is 50% green, 25% red and 25% blue. So he claims that the population is 50% green, 25% red and 25% blue.
Wooster's sample is 25% green, 25% red and 50% blue. So he claims that the population is 25% green, 25% red and 50% blue.
That's quite a big difference. Who's closer to being right and why?

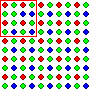
The reason Jeeves's argument is better than Wooster's argument is that argument Jeeves's sample is big enough to swallow it's imperfection in the mixing of the population (which means that his sample is representative of the population) while Wooster's sample is so small that it's imperfection crosses the sample border, distorting the result (which means that his sample isn't representative of the population). Are these samples too small? Well that depends on what we know about the structure of the population.

Sample Size

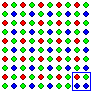
We saw above that it's possible to have a sample that's way too small to accurately represent the population it's taken from. However, it is sometimes the case that a population is structured in such a way that even a small sample can be perfectly representative, if it's taken the right way. A population is not always arranged as a chaotic mixture of individuals. Some populations are arranged in such a manner that we can take a very small sample with absolute confidence that the result will perfectly represent the composition of the population. For instance, consider the population of dots shown below. Imagine that we know that the population is structured in the way shown, but we don't know the colors of any of the rows. Now imagine we take the very, very, very, very small sample of exactly four dots comprising the first dot in each of the first four rows, as shown in the top left corner of the image. That's a sample of four out of four thousand. That's one per thousand, which means one tenth of one percent, or 0.001. Is that too small?

Our sample comes out 50 percent red, 25 percent blue and 25 percent green. Given that we know the structure of the population, what are the chances that the population is 50 percent red, 25 percent blue and 25 percent green?

Therefore, the following argument is very bad. (Technically, it commits what we call a red herring fallacy:)

It hasn't been proved that the dots in the picture above are 50% red, 25% blue and 25% green because the sample upon which that generalization is based is only 0.001 of the population, which is waaaaaaaay too small a sample.

The key fact here - the thing that makes this argument bad - is that the population is completely structured in alternating homogeneous rows of red, green, red and blue dots. It is this highly organized structure that allows a miniscule sample of just four dots to perfectly represent the composition of the whole population.

As a matter of fact, there is no limit to how small a sample can be. To see this, imagine a population of infinitely many dots, part of which is shown below. (The rest of the dots extend off your screen to the right.) This population is structured as you see here, in four rows of dots, each row being composed of dots of exactly the same color.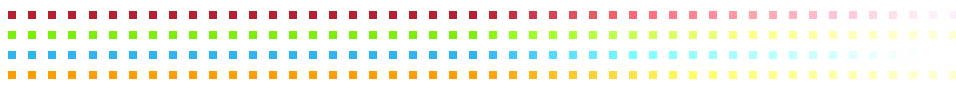

How big a sample do you need to tell the composition of this population? Will four dots do? It will if each of those four is the first dot in it's respective row. Now, that is an infinitesimal sample, which means it's equal to one divided by infinity, but that doesn't matter, because the population structure makes that proportionally infinitesional sample perfectly representative of the whole.

There are two lessons here. The first is that even an infinitely small sample can be representative if it's properly taken from a population that has the right structure. The second is that it's possible to fail to convey the most important facts about this situation. To see this, think three things. First, think about a particular population that is very similar to the one pictured above. Second, think about two opposing arguments about that population. And third, think about two different critiques of the weaker of those two arguments. It is those two critiques that I want you to focus on here.

Key Fact: The population is arranged in equally-sized rows of indentically-colored dominoes.

Perfect Mixing

Another way to get an accurate result with a very small sample is if a population is perfectly mixed. Imagine another infinitely large population in which individuals are so perfectly mixed that every part of the population looks like the following picture. (Notice that this is NOT a random distribution of dot colors. It's a carefully structured distribution. A random distribution would be unevenly mixed, not smoothly mixed like this one.)

Try to find a four-square group, or a contiguous line of four dots that isn't a representative sample for this population.

Now imagine blindly picking dots from random places scattered through the population. How many would you have to pick to guarantee a representative sample? Not many!

Now imagine you work for a petroleum company. You check the composition of oil products so the company can decide how each tanker load will be processed. Your company's tankers contain a pumping system that circulates the oil between all the tanker's oil-carrying compartments. All the oil is moved and turbulance from the pumping process mixes the oil products so thoroughly that every centiliter in that tanker is absolutely identical to every other centiliter in that tanker. Given that a litre is one hundred centiliters, would one liter be a big enough sample to test the composition of the oil mixture in a tanker holding a billion liter of oil products?

The point here is that small sample size may make the sample untrustworthy, but there may be special circumstances that make this particular sample an accurate representative of the population, even though it is way smaller than we would normally accept as a good sample.

Estimating Sample Size: Variables and Values.

If 1% can be an adequate sample, 50% can be inadequate. Imagine that Noah was an educational administrator who had to rely on state grants for his funding. God issues a grant that will allow Noah collect two of every animal, but Noah's immediate superiors insist he spends half of God's money on computers. Thinking outside the box, Noah adapts to the situation by only including one of every animal. What if aliens later came across Noah's Ark bobbing on the flood waters, how big a sample would they need to accurately represent the animal passenger list? Say they picked 50% of the animals at random. Would that give an accurate picture? Would 90% be enough to give a picture that was accurate to within 1%?

When we're worrying about sample size for a perfectly random sampling method, it is sometimes useful to talk about variables and their values. Consider Noah's Ark, but this time without any middle-management between god and Noah. Noah marches on board two-by-two, one couple of each kind. In this situation, sex and species can both be considered variables, each with its own characteristic range of values. Sex is a variable with only two values, and thus a sampling argument concerning the sexes of the animals would only need a fairly small random sample. Species, on the other hand, is a variable with thousands of possible values. Given that Noah's Ark contains only two of each kind of animal, a sampling argument concerning the distribution of species on the Ark would need a sample size of considerably more than fifty percent, if it was based on a truly random sample. (A non-random sample could do it accurately at only fifty percent, if the sample was chosen in the right way.)

How big is big enough? Firstly, the issue of whether a particular sample is big enough doesn't depend on what percentage of the population is included. If the above well-mixed population was only four individuals large, only a 100% sample would be big enough! Anything less than four would leave out at least one color! If the above population was 8 individuals, a 50% sample would do. If it was 16, a 25% sample would work. If it was 32...

The minimum necessary sample size depends on the number of different relevant properties individuals can have, and on the degree of mixing in the population. In the well-mixed population above, the number of different relevant properties is four, because there are four colors, and the population is perfectly mixed. If the number of different properties was larger, or if the population was less well mixed, minimum necessary sample size would be larger.

Finally, I have noticed that some students have a tendency to say that a sample size is too small when they cannot think of anything else to find wrong with the argument, or where the sample size is ten percent or less. Don't do this. If you cannot think of a reason why this particular sample is too small for this particular population, given this particular sampling method and the structure of this particular population, then the sample size is not too small. Arguments are only bad when there are specific reasons to find them bad. Saying that the sample size is too small when you can't think of anything else is never a good idea.

Sample Age

Imagine you are an atmospheric scientist studying inertium monoxide levels in the atmosphere at various points in history. Like the rest of Earth's air, intertium monoxide does not react with any other gases in Earth's atmosphere. Say that because of the way inertium monoxide is produced and distributed, the level of inertium monoxide in Earth's atmosphere at any point on Earth is never more than ten percent more or less than the global average at that time. (If today's global average is 1%, there's nowhere on Earth where the inertium monoxide levels are lower than 0.9% or higher than 1.1%.) You recover an air sample that's been held absolutely isolated for three thousand years at the base of a really old glacier. (They can actually do this for samples that are several hundred years old.) The sample contains 10% inertium monoxide, so you can conclude that three thousand years ago, Earth's atmosphere held a global average of between 9 and 11 percent intertium monoxide.

Is the sample too old? Not if the sample was absolutely isolated! Remember, there's nothing in Earth's air that inertium can react with, so the sample can't change over time. Isolation prevents sample gasses from escaping and gasses from later atmospheres from getting in, so it can't change that way either. So, in this case, a three thousand year old sample is enough for a good generalization, provided that all the other factors are taken care of. Notice however that we can't use this sample to generalize about today's atmosphere. Atmospheres can change quite spectacularly over time. Imagine trying to generalize about the air in Los Angeles today based on an air sample taken in 1902! This is why I use the term obsolete, which means that we know that conditions have changed, so that the sample is no good anymore. A sample can be very old without being obsolete, and a sample can be obsolete without being very old at all.

Here's a real-life example. More than about 4 billion years ago, the solar system was nothing but a widely spread out mass of gas and dust particles which was slowly but surely organizing itself into bigger and bigger clumps, many of which banged into each other to make larger clumps. Our Earth was one of those lumps. While the Earth was first forming, it was hot and mostly molten, so the heavier materials gravitated to the center of the lump and the lighter materials were forced up to the surface. The heaviest materials became the Earth's core. Just before the Earth finished forming, a really big lump smashed into it hard enough to kick some of that core material up to the surface on the other side of the Earth. 4 billion years later, scientists found some of that material, figured out what it was, and used it to figure out the exact chemical composition of the Earth's core. Think about it. Not only is the few pounds of material they used a tiny, tiny sample relative to the total size of the Earth's core, that sample is 4 billion years old. However, the Earth's core has been subjected to enormous heat, pressure and mixing by convection, so it's extremely well mixed. Furthermore, there's no known substance that could turn into nickel-iron over any timescale, so we have good reason to think that the composition of that core has not changed in 4 billion years, and that the composition of the pieces of core material that the scientists used hadn't changed either. So in this case, a sample that's about as old as a sample can get on this planet turns out not too old!

Of course, saying "That generalization's no good because the sample's 4,000,000,000 years old!" is a red herring fallacy.

Key Fact: There isn't any substance out there that will turn into iron and nickel under these conditions, not even if you give it billions of years to do so.

And, conversely, having a very very recent sample does not guarantee a logically compelling argument. Some populations change very rapidly. Think about trying to do a generalization about present computer use, or present cell phone use, or home recording equipment, based on data from 1950.

Again, we always need to think about the age of a sample, but we still can't dismiss a generalization based merely on age. If we have good reason to think that the sample hasn't changed since it was taken, and that either the population hasn't changed either, or the generalization is about what the population was like at the time the sample was taken, then the generalization is fine even if the sample is old. Some samples become obsolete very quickly, some stay good for a very long time indeed.

Randomness

People sometimes say that all samples have to be taken randomly, or they're no good. This isn't exactly true. There are circumstances where the population structure will make it possible for a small non-random sample to be much more representative than an equally sized random sample. Consider another set of dominoes, arranged in ten identically sized and colored rows so that each row is a different color from every other row. Selecting one domino from each row will give an exactly correct picture of the overall population. Selecting ten dominoes at random from the overall population has only a very, very, very small chance of getting an accurate picture because of the very, very high chance of getting two or more dominoes from the same row.

Sampling Method

A generalization can only work if it uses a sampling method that is completely independent of the feature being tested. If the sampling method is at all sensitive to that feature then it will tend to either seek out or avoid members of that population that have that feature. Either way, the result will be skewed.

Some people call this sensitivity "bias." I don't like that terminology. For one thing, "bias" has more than one meaning, and not all it's meanings have anything to do with the accuracy of generalizations. And a sampling method can be very biased while still giving a very accurate result. The thing to remember about "bias," is that it only counts if the bias is relevant to the feature being tested. If you're sample is biased, but you can show that the bias has nothing to do with the feature being tested, then that bias gives you no reason to throw out the study.

Let's go back to assessing the tipsiness of Hogmanaying Scots. Say we happen to know the names and addresses of three significant groups of Scots. We know the names and addresses of all Scottish accountants, all Scottish teetotalers, and all Scots who have been convicted of drunk driving at least three times. Say we examine every member of each group to see whether he or she got tipsy last Hogmanay. And say we got the following results.

1. 67% of all Scottish accountants got tipsy last Hogmanay.

2. 0% of all Scottish teetotalers got tipsy last Hogmanay.

3. 99% of all Scots who have been convicted of drunk driving at least three times got tipsy last Hogmanay.

These results can't all be representative of the whole Scottish population. At best, only one is right. So which of these figures is more reliable? The answer is, whichever one is least sensitive to the feature being tested. What do accountants have to do with tipsiness? Nothing that I can think of! But teetotalers are people who habitually abstain from alcoholic beverages. (Strange, but true.) So of course none of them got tipsy on Hogmanay. Are all Scots teetotalers? I don't think so! So that sample is definitely dependent on the feature being tested. On the other hand, habitual drunk drivers can be expected to drink more than regular Scots, so that sample is dependant too. (Notice that one of them is negatively dependent, in that it avoids the feature being tested, and the other is positively dependent, in that it seeks out the feature being tested.) So, since we can't find an obvious link between accountancy and tipsiness, sample number one is the only independant sample.

Key Facts

Key Fact 1. Being an accountant has nothing to do with getting tipsy. (Makes the sample good.)

Key Fact 2. Teetotallers don't drink, and this is a question of drinking behavior. (Makes the sample bad.)

Key Fact 3. Drunk drivers can be expected to be heavy drinkers, and this is a question of drinking behavior. (Makes the sample bad.)

It can be very difficult to tell whether or not a sampling method is dependant. The trick to telling whether or not a sample is dependant is to look at the way the sample was obtained. If it was obtained in a way that has nothing to do with any of the possible outcomes of the study, then it is not dependent. If, however, the method by which the sample was chosen is logically connected to the properties the sample is supposed to test for, then that's a dependency, and the argument is no good. Consider the following sampling methods.

1. Testing American reactions to the war in Iraq by mailing questionnaires to the membership of the American Pacifists Association.

2. Testing the distribution of blood types across the United States by taking blood samples from members of the Mayflower Society, a group which restricts its membership to people who have at least one direct ancestor that came over to America on the Mayflower.

3. Assessing the bodily proportions of 18th-century Americans by measuring antique clothes preserved by historical societies.

Obviously, the first sampling method is no good because (key fact) we would be taking our sample from a group that is already self-selected to be against any war. The second sampling method is also dependent because (key fact) the Mayflower passengers came from a very small region in Europe whereas the vast majority of other immigrants to the United States came from other regions, and continents, and (other key fact) blood type is very highly correlated with ancestry. Finally, there is the (key) fact that until recently, good quality clothing (the kind that is likely to be preserved) tended to be reused as long as it could be made to fit new people. Larger clothing was easier to alter than smaller sized clothing, so it tended to be reused until it wore out. Smaller sized clothes tended to be put away in the hope that someone would come along who could use them, so smaller sized clothing is much more likely to have been preserved than larger sized clothing. Therefore, the third sampling method is also dependant.

Fallacies

Fallacies are specific things that can go wrong with arguments. I like to think of them as bad arguments that some people commonly mistake for logically compelling arguments. Here I will talk about those fallacies I think most relevant to sampling arguments. Some of them will also be important in other contexts, while others will only be important when we specifically discuss sampling. Now, there are a couple of fallacy names that would be helpful to know before we talk about how to evaluate sampling arguments. They are hasty generalization and red herring. "Hasty generalization" is the name for any generalization where the sample logically fails to support the conclusion. "Red herring" is the name for any argument where a key premise is logically irrelevant to the truth or falsity of the conclusion.

Hasty Generalization

The term "hasty generalization" is really too vague to be useful, so I break it down into four separate fallacies: Inadequate sample, Obsolete sample, Dependant Sample and Anecdotal Evidence. The key to determining whether an argument commits hasty generalization is to ask whether the available facts allow a reasonable alternative explanation for the state of the sample. Here are the generalization fallacies in more detail.

Inadequate sample. The population clearly has not been shown to be so evenly mixed that a sample of this size can be reasonably assumed to properly represent the population. Remember that 1% can sometimes be big enough while 90% (or more) can sometimes be too small.)

The International University on the Moon has over 20,000 students from all of Earth's 140 or so countries. I've taken an absolutely random sample of 10 students out of those 20,000, and 2 of those students were from Armenia, so we know that 20% of the students on the Moon are from Armenia.

Imagine that 143 countries are represented on the moon. In that case, a ten-student sample will miss at least 133 of those countries. This means that a sample needs to be at least 143 students to have a hope of being adequate, and we would probably want about 300 to have anything like a reasonable sample. (Key fact: There's about 140 different countries.)

Obsolete sample. The population clearly has not been shown or clearly cannot be assumed to be unchanged since the sample was taken, so it's clearly possible that the population has changed, making the generalization out of date. (Remember that 15 billion years isn't necessarily too old while an hour isn't necessarily recent enough.)

In 1843, 35% of all American families owned at least one buggy whip, that means that there's a 35% chance that there's a buggy whip in your house.

Considering that Americans almost completely stopped driving horse-drawn buggies once automobiles became widely available, information from when buggies were widely used is not going to represent present transportation related realities. (Key facts: Buggy whips are only needed by people who drive buggies, which are drawn by horses, and almost nobody uses horse-drawn transport nowadays.)

Dependant sample. The sampling method clearly has not been shown or clearly cannot be assumed to be random with respect to the feature being tested, so that it's clearly possible that the sample fails to accurately represent the population. (Remember that a "bias" that is not relevant to the feature being tested cannot be a problem.)

Did you know that they recently held a school assembly where they publically interviewed 20 randomly chosen graduates of the schools Substance Control and Abuse Rejection Enterprise program, and 100% of those SCARE graduates reported that they've never tried drugs!

Considering that drugs are illegal, and that a student who publically admits to having tried drugs is going to be in a lot of trouble, it wouldn't be surprising if some or all of those students were lying. (Key fact: people tend to give answers that please the questioners, especially if the questioners have power over them.)

This too counts as a counter argument. If my analysis turns out to be bad, then it's a bad counter argument. But it's still a counter argument, whether it's good or not.

Anecdotal Evidence. Here the arguer fixes on a particular story and tries to use it to support a generalization. The problem is that the anecdote could easily have been picked precisely because it supports the point the arguer wants to make, and might be screamingly atypical of the population he wants to generalize about.

Handgun Control, Inc. faked statistics on gun violence. That proves all gun-control activists are liars.

Key fact: That's just one incident, which could easily be the only such incident. No general survey is cited here.

That Mensa member tried to murder the people next door with thallium, and wrote snotty articles about it in the Mensa newsletter. That proves that all smart people are evil.

Key fact: That's just one incident, chosen because it's about a "smart" person attempting murder. There are thousands of other Mensa members and millions of other smart people.

Of course America was as deeply involved in witch burning as Europe was. Didn't you hear about the Salem Witch Trials?

Key fact: That's just one small series of incidents that might easily have been America's only literal witchhunt.

Keagan. Okay, I'll admit that some cops are racist. But you'll have to give me some pretty convincing evidence before I'll believe that all cops are racist.
Aylin. But didn't you see the Rodney King videotape? That videotape showed five white LAPD officers repeatedly beating a prone, unresisting black motorist. They just kept whaling on him, hitting him over and over again. It was a savage, stupid beating that King would not have gotten if he had been white. That proves all cops are racist thugs

It's true that Aylin gives a very salient example. That is, he gives an example that sticks out, or otherwise makes a deep impression on the listener. But salience isn't significance, and an example can be very salient without being at all representative.

Key Fact: This is exactly one incident that was chosen precisely because it supports the arguer's opinion, which makes it perfectly possibile that this was one of only a very few racist attacks by police officers.

By the way, did you notice that Keagan's argument relied on a claimed lack of evidence, and that Aylin's argument claimed to supply that evidence. This made Aylin's argument one of those rare cases of a direct argument that's also a counter argument. (Remember, this can only happens against an argument based on the claim that there's no evidence for something.

The Fallacy of Validation by Examples

I was once caught in a dispute with a person who obviously considered himself intelligent, educated and reasonable. At one point, this person made a sweeping and controversial generalization based on no evidence whatsoever. I asked him if he could back this up. His response was "let me validate with examples," by which he meant he was going to give me a series of cases each of which would be claimed to be an example of his thesis, and this was supposed to be logical evidence that he was right. Here is a (completely hypothetical) example of "validation by examples:"

Samantha. You know of course that the media has a conservative bias.
Lauren. Um, do you have some kind of survey or university study of randomly chosen news stories in which actual reporting was found to put a more postive spin on similar sets of facts when a conservative was involved than when a liberal was involved, because that's what you'd need to prove actual bias.
Samantha. Rubbish, you don't need that. I can validate this with examples. You remember when the media reported that liberal Democrat senator Gropemeister tended to get touchy with women who visited his office?
Lauren. Yeah, that was pretty creepy!
Samantha. Well the only reason they made such a big deal of it was because he was a liberal! If he'd been a conservative they'd have held back on front page stories describing the nasty details , the way they did when conservative Republican Mayor Longsuffering of Buffalo was caught doing the same thing.
Lauren. But didn't Longsuffering turn out to have been falsely accused by a mentally disturbed ex-employee? And he's only a medium city mayor, not a US senator, so...
Samantha. And I've got dozens of other examples. What about Representative Random and the . . .
Lauren. Oops! Look at the time. Gotta go.

If you look carefully at Samantha's arguments, you can see two distinct logical errors. The first is, of course, that she is "supporting" her claim with a set of anecdotes that she chooses herself rather than by properly collected and interpreted independent evidence. The second is that she's not just giving anecdotes, she's also adding in her own assumptions about what they mean. When she finds negative coverage of a liberal, she assumes that the negativity must be the result of bias, and likewise less negative coverage of a conservative must be a result of bias. Thus she builds her assumption of bias into her interpretations of her data, and thereby assumes the very thing she's supposed to prove. (And you can see me as mounting a counter argument here.)

Red Herring

Apart from the fact that Red Herring is a very common fallacy, I mention it here because people often attack sampling arguments on the basis of sample age, sample size or sampling bias when these issues are completely irrelevant to the strength of the argument. Therefore, an arguer commits red herring if:

1. His criticism of a generalization is based on sample age when we have no reason to think that either the population or the sample has changed since the sample was taken.

2. His criticism of a generalization is based on sample size when we have no reason to think that this particular sample is too small for this particular population.

3. His criticism of a generalization is based on a bias in the sampling method when we have no reason to think that this particular bias has anything to do with the feature we're testing for.

Logical and Illogical Thinking

Finally, I want to introduce a distinction between "logical" and "illogical" criticism of an argument. In this text, I tend to use the word "logical" in a pretty broad sense, to mean any kind of thinking that has a chancemight help us to figure out the truth of the matter. Thus, I would say you're thinking logically if you're paying attention to the actual features of the argument, including details of the evidence offered, and the logical relationship that might hold between that evidence and the conclusions offered to explain it, even if, at that point, you happen to be making a mistake about that evidence or relationship. In other words, you're thinking logically if you are looking at things that do actually sometimes go wrong with arguments.

On the other hand, you are not thinking logically if you simply assume that somebody is wrong, or speculate about people's feelings or motives, or smugly asserts that you're above it all, or in any other way ignores the evidence or logic of someone else's argument.

Aussuming that Mutt has given an actual argument of some kind (however flawed it might be), the following are all examples of clearly illogical thinking. (The person who utters such inanities as this may say other things that are sensible, but whatever else that person says, the following statements are all absolutely illogical.)

Mutt's argument is bad because Jeff''s argument is good.
Mutt's argument is bad because Jeff proves his conclusion is true.
Mutt's argument is bad because he does not want to accept that Jeff's conclusion is true..
Mutt's argument is bad because he is only stating his opinion.
Mutt's argument is bad because Jeff has the facts.
Both arguments are bad argument I look at this whole discussion and I just laugh because it's all so ridiculous to me.

Number one is illogical because the mere assertion that one argument is good cannot possibly prove anything about any other argument. Similarly, number two is illogical because the mere assertion that one person has proved something (which can only happen from a compelling argument), can never prove anything about anybody else's argument. Number three is not only illogical (because speculating about people's feelings cannot ever prove anything), it is also slanderous because it asserts without evidence that someone formed their belief illogically on the basis of feelings rather than facts. Number 4 is illogical for similar reasons. If Mutt is presenting any kind of argument at all, it is simply fales (and dishonest) to say that he's only stating his opinion. Number five is wrong in more subtle way. Ignorant and foolish people tend to use the wor "facts" simply to mean "things I believe," (and the word "opinions" for "things I don't believe"), which means that the phrase "Fred has the facts" is basically the same as "I believe Fred," which of course has absolutely no logical force. Number six might well be the stupidest thing anybody ever says about an argument. In my experience, it is only ever said by people who do not actually understand anything about the arguments they are dismissing as "ridiculous." If someone says this phrase to you, ask them pointedly to explain to you which side is right, and why, If they can't give a logical reason why one side is right and a logical reason to think that the other side has failed to prove it's points, then they are an idiot who mocks things they don't understand.

A good rule of thumb to identify illogical criticisms is to ask yourself if the "criticism" helps you understand what precisely is supposed to be wrong with the criticised argument. If the speaker is basically just especting you to take their word that the "criticised" argument is bad, then this "criticism" is not actually criticism in the sense of providing a critique of the argument.

of exposing an issue that

Exercises

Many of these exercises consist of opposing pairs of arguments. They're called "opposing" because the arguers disagree with each other, and so each one in some way opposes the claims of the other argument.

(Answers at the end of the chapter.)

1. Keyshawn. My survey says that Americans don't particularly care about the proposal of adding a small federal tax on all computers and modems sold in the United States. My people visited over a thousand grocery stores in all kinds of neighborhoods in all fifty states. They selected people from all walks of life and all income levels. They asked twenty thousand people what they thought about the proposed tax. Most hadn't heard of it, and didn't care about it when they did hear. Those who cared were evenly distributed between mildly for and mildly against.
Dominique. Well, your information is wildly wrong. My company found a way to reach one hundred thousand people in a very short period of time. We did an e-mail poll of names selected at random from a very large database of people who are considered preferred customers by our three largest computer retailers. Ninety-five percent of our respondents had heard of the tax, and eighty percent of all respondents were strongly against it, so eighty percent of Americans are strongly against this tax.

Select the best critique of this dialog from among the following.

A. Keyshawn's argument is bad because he does not prove that Americans don't particularly care about a small federal tax on all computers and modems sold in the United States.

B. Keyshawn's argument is very weak. Just because 20,000 people from all walks of life and income levels picked randomly from outside grocery stores in all kinds of neighborhoods didn't care about the tax doesn't mean that Americans in general don't care about the tax.

C. Keyshawn's argument is bad because of the small sample size.

D. Dominique's argument is bad because her sample was taken by e-mail, so it excludes people who are not computer users, and it includes only people who are preferred customers of computer retailers, which means that it includes only people who are heavy computer users. Since the feature in question is attitude towards a tax on computer equipment, this is not an independent sample.

E. Dominique's argument is bad because she does not understand that Keyshawn's sample is not too small.

F. Dominique's argument is bad because she is only stating her opinion whereas Keyshawn has the facts.

2. Deion. A lot of Muslims live in my neighborhood. There's a mosque just up the street from my house, and Muslim people visit here from all over the world. So I meet many, many Muslims from all different countries as neighbors and friends. None of them want to forcibly convert anyone to Islam. None of them know anyone who wants to forcibly convert people to Islam. In fact, no Muslim I know or know of knows of anyone who wants to forcibly convert people to Islam. So I don't think it's true that a majority of muslims want to forcibly convert people to Islam.
Aryanna. You're so naive. Haven't you heard of the muslim wars of conquest in 632-750 AD? Every Muslim in existence then was committed to forcibly converting everyone in the world to Islam. And they acted on this commitment, marching in massive armies into Arabia, North Africa, Europe and Asia. They converted everyone they met at sword point, and killed everyone who wouldn't convert. These actions were universally applauded in the Muslim world, so a majority of Muslims strongly support the conversion of people to Islam by force.

Say which of the following is the most appropriate critique for the weakest argument in this dialogue?

A. Deion's argument is bad because a majority of Muslims strongly support the conversion of people to Islam by force.

B. Deion's argument is bad because Aryanna proves that Deion's argument has many logical flaws and problems. She proves that his argument is not logically sound and that it commits several logical fallacies.

C. Deion's argument is bad because who are we to say whether Muslims want to convert people by force or not?

D. Aryanna's argument is bad because realistically, modern Muslims are not going to want to convert people to Islam by force.

E. Aryanna's argument is bad because she is using information from over a thousand years ago. Societies can change very rapidly in only a few decades, and it is unreasonable to think that present day Muslims must have the same attitudes as Muslims who lived a thousand years ago.

F. Aryanna's argument is bad because the armies of conquest were actually only a very small proportion of the total Muslim population. The Muslim world that time included several million people, and the armies were only a few tens of thousands of people. This means that only around one percent of Muslims took part in the wars of conquest, so it's ridiculous to say that a majority of Muslims at that time supported the use of force to convert people.

For each of the following argument pairs, work out which argument is weaker by applying the correct rules of analysis, and then write your own, original critique of the weaker argument.

3. Deangelo. I don't think many people believe in Bigfoot nowadays. A very reliable public opinion company has been taking belief surveys every year for the last forty years. Forty years ago about half the population took Bigfoot seriously, but since then the percentage has slowly and steadily declined. The last survey was eight months ago, and it found that only 20% of Americans think Bigfoot might be real.
Micah. Well, your information is wrong! Just a few weeks ago, the network of Fake-Jamaican Psychics gave a telephone survey to everyone who called in for psychic or astrological advice. They had 27 million callers, and 74 percent of those 27 million asserted that they firmly believed in the reality of Bigfoot. Two weeks ago is very recent. 27 million is an enormous sample for this kind of poll. No other opinion poll has used a sample size of more than about 10,000, and many of those polls are considered extremely reliable! So we can take it as proved that about 74 percent of Americans believe in Bigfoot.

4. Pierre. The latest AARP survey says that American seniors are living longer and healthier lives than ever before. Old people make up around 10 percent of American society, and respondents to the AARP survey turned out to be both significantly healthier, and to have on average lived considerably longer than a demographically identical group surveyed only five years previously. I think this survey is reliable, because it is based on responses from nearly the entire membership of the AARP, which is of course composed entirely of seniors, and was supervised by the best statistical survey analysts available.
Sonya. You're forgetting one thing. The AARP only makes up just over 5 percent of the American population. How can you make any kind of serious generalization based on a sample that is just 5 percent of the population?

5. Freddie. I've got to say that in a weird way my respect for conservatives has increased during the present crisis. I've talked to a lot of conservatives about the present situation and most of them present very reasonable case for their own side. They are not a bunch of bloodthirsty warmongers, or knee-jerk jingoists who support any military action no matter how ill-advised. Rather, the overwhelming majority of the ones I've talked to are extremely upset by what they see as the necessity for military action, and although I firmly disagree with their reasoning, I have to say that most of them have taken a great deal of time and effort to think through the issues. Let's face it, there's plenty of intelligent conservatives out there.
Martina. I don't know how you can say that there are plenty of intelligent conservatives out there. I've listened to A.M. radio dozens of times and every Conservative talk show host I've ever heard has been an ignorant, irrational blowhard who does nothing but disparage liberals without ever bothering to find out what any actual liberals are actually saying about anything! Yes, there's a lot of variety in these talk show hosts. There are loud blustery idiots, and quiet vicious idiots, and pedantic boring idiots, and self-important patronizing idiots. But there's nobody who's willing to even begin to talk about the real issues and arguments!

6. Gino. I'm worried about the sulfur content in that load of crude oil you've got tied up at the docks there. I've just heard that it has come from an oilfield where the crude usually has a high sulfur content. That's a large capacity supertanker you've got there with over a hundred separate storage tanks, so if I load all your oil into my refinery, I could end up contaminating my entire works with sulfur products.
Elsa. I anticipated your concern, and I dipped out this five gallon sample from the No. 42 hold before I came over to your office. Your own lab has certified that it has a very low sulfur content, so you don't have to be concerned about the sulfur content of my oil.

7. Kathy. My cousin just came back from a business trip to Viet Nam. She said the people were nice enough, but she thought there was an undercurrent of resentment and suspicion towards Americans among most of the people she dealt with there. I guess the Vietnamese over there are still not quite as friendly towards American business people as people in other parts of the world.
Madisen. Your cousin is dead wrong. All the people in Viet Nam love and admire Americans. After the Japanese occupiers surrendered, Ho Chi Minh and other Vietnamese leaders welcomed the Americans in as liberators and supporters of Vietnamese independence. Why, love and admiration for America was part of the Vietnamese language at that time. People used to say "oh, to be as rich and wise as an American!" Does that sound to you like people who are suspicious and resentful of Americans?

8. Gideon. You know you thought that we would never be able to get any kind of accurate idea about the composition of the Earth's core? Well, scientists have discovered that a massive meteor or asteroid whacked into the Earth while it was still relatively hot, and the shock wave kicked up some of the core material through the soft mantle and crust. The crust was solid enough by then to hold this material in place. Although some of the material was exposed by erosion, a lot of it was protected from the elements by being buried in stable rock structures. This material was shielded from water and other kinds of erosion, and scientists were able to recover a sample. The samples were 90% iron and 10% nickel, there is nothing that can turn into nickel-iron over time, and nickel-iron won't turn into anything else if it's kept away from water and air down in the core, so the Earth's core is 90% iron and 10% nickel
Anaya. Wait a minute! That asteroid impact must have been over ten billion years ago. Ten billion years must be the oldest sample ever taken in science! We commonly discard hundred-year-old samples as too old, and we don't even look at some thousand year old samples. Your sample is ten million times as old as that, so it can't possibly be any good.

Study Questions
9. What do we call a small, examined group chosen from some larger, otherwise unexamined group for purposes of answering some question about the composition of the larger group?
10. What do we call that larger group?
11. What to we call the particular aspect of the population we're looking at?
12. What do we call it when the small group is very, very likely to have the same composition as the larger group?
13. What do we call it when the small group is not likely to have the same composition as the larger group?
14. Is it true that an argument that is based on a sample that is very old is always a hasty generalization?
15. Is it true that an argument that is based on a sample that is very small is always a hasty generalization?
16. Is it true that an argument that uses a non-random sample is always a hasty generalization?
17. Is it true that a very old sample can still be a good sample?
18. Is it true that a very small sample can still be a good sample?
19. Is it true that a sample that was not taken randomly can still be a good sample?
20. Is 1% always too small? Is 50% always big enough? Explain
21. Is 1000 years always too old? Is 1 year always recent enough? Explain.
22. Is it true that some populations are too complicated to be properly represented even by a very large sample?
23. Is it true that some populations change too rapidly to be properly represented by even by a very recent sample?
24. in the context of sampling arguments, what is the difference between hasty generalization and red herring?
25. Explain the three ways to commit red herring when criticizing a generalization.
26. What are the three ways a sampling argument can go wrong?
27. What does it mean to say that a sampling method is "dependant?
28. What kinds of biases are a problem? What kinds of biases are not a problem?

For more practice, you can download and do the practice/makeup exercises. (Make sure the document margins are set to 0.5 inches or narrower.)

Exercise Answers

1. Only critique D is any good here, because it is the only one that mentions the key fact that the poll was taken exclusively from people who buy a lot of computer equipment. None of the other answers gave any reason at all to think that the argument they referred to had any logical problems. Critique A fails because all it does is say that Keyshawn does not prove his point without giving any reason to think that Keyshawn has failed to prove his point. Critique B actually has exactly the same problem, except that it takes the time to describe Keyshawn's argument. Saying that an argument does not work is not the same as proving that it does not work. Critique C fails because it does not give any reason to think that Keyshawn's sample is too small for this population. Critique E is not only bad, but insulting since it without foundation accuses Dominique of failing to understand the situation. Instead of giving reasons against Dominique's argument, critique E purports to look inside her mind and find her wanting. This is never a legitimate argument. Critique F is, of course, the worst kind of muddy thinking.

2. Critique E is correct. It is the only critique that focuses on the key fact that the data Aryanna uses is over a thousand years old. Critique A simply repeats the opposing conclusion without giving any criticism of Deion's argument. Critique B is worthless because it simply makes a series of unfounded claims about Deion's argument. Critique C is not a critique but an insult. It simply repeats the opposing conclusion with an unfounded accusation that Aryanna is being unrealistic. Critique F completely misses the point of Aryanna's argument. She was not arguing that most of the Muslims at that time took part in the wars of conquest, she was pointing out that most of the Muslims at that time supported the wars of conquest.

3. Micah's argument is weaker because his sample consists entirely of people who believe in psychics and astrology. Like Bigfoot, these are both things that mainstream science discounts, so this group is composed entirely of people who tend to disagree with mainstream science about psychics and astrology. This makes Micah's sample unrepresentative because the American population also includes large numbers of people who accept mainstream science and therefore disbelieve in things like psychics, astrology and Bigfoot. Thus the proportion of people who believe in Bigfoot is likely to be smaller in the general population than it is in Micah's sample of people who believe in psychics and astrology. (The fallacy here is dependent sample. The key fact here is that people who believe in psychics and astrology are much more likely to believe in Bigfoot than people who don't believe in psychics and astrology.)

4. Sonya makes two mistakes. First, she thinks that 5 percent is too small a sample. In a properly conducted study, 5 percent is plenty. However, Sonya makes another mistake. Pierre's generalization does not cover the whole American population. It just covers the 10 percent that are seniors. 5 percent is half of 10 percent, so Pierre's sample is 50 percent of his population, not 5 percent. (Sonya's fallacy is a red herring, because she is talking about something that is not relevant to the issue. The key fact here is that Pierre's survey covers half of the population he's talking about, which is an enormous sample when you're talking about a variable that only has two possible values: healthier, and not healthier.)

5. Martina's argument is weaker because her sample is dependent. Her sample might be thought to be inadequate as well because, while there are tens of millions of conservatives in this country, only a hundred or so have radio shows. However, we are talking about a variable that has only two values, intelligent and unintelligent. If this sample was truly random, a sample size of one hundred would be perfectly adequate. However, we have reason to think that the sample is dependent. First, we have Freddie's unopposed evidence that intelligent conservatives do exist, and there is the fact that talk show hosts are selected on the basis of entertainment value rather than intelligence. It is a sad fact of modern society that idiots are often considered to be more entertaining than intelligent people, so it is perfectly reasonable to think that the people who select talk show hosts have a strong preference for idiots. (The fallacy here is dependent sample, and the key fact is that talk show hosts are expected to be entertaining rather than intelligent.) Another way to understand this exercise is to look at the difference between the two conclusions. Both samples are recent, both are small, and neither is randomly chosen from the population. But look at the difference in their conclusions. Freddie argues that there are "plenty" of intelligent conservatives, while Martina argues that there are no intelligent conservatives. Freddie's conclusion could be true, and Martina's conclusion false, even if AM radio is populated by idiots, since only a few conservatives have radio shows. However, Martina's conclusion is that no intelligent conservatives exist, which would imply that the intelligent conservatives that Freddie is talking about do not exist. Since Martina has given no reason to think that there is anything wrong with Freddie's survey, we should conclude that the intelligent conservatives he talks about do in fact exist. they do exist, Martina's conclusion must be wrong, and her argument is a hasty generalization from a small sample. Since Freddie's conclusion is much weaker than Martina's, his argument is much stronger.

6. Elsa has the weaker argument. Her sampling method is inadequate because, firstly, the population consists of one hundred separate storage tanks and there is no guarantee that the population is perfectly mixed. Secondly, Elsa chose the sample herself, and so there is no guarantee that he did not accidentally select the one tank in the tanker that was free of sulfur. (And there is also the possibility that she unconsciously selected oil from a tank she subconsciously knew to be low in sulfur.) (The fallacy here is inadequate sample. The key fact is that there is no guarantee that the oil in the whole tanker is perfectly mixed.)

7. Madisen's argument is weaker because she is using data from the period just after World War II, which was over sixty years ago, and public attitudes can change considerably in that amount of time. (The fallacy here is obsolete sample, the key fact here is that her sample is over sixty years old, and attitudes can change enormously in that amount of time.)

8. Anaya's argument is weaker. The amount of time since the asteroid impact does not matter because there is no known substance that could have changed into nickel-iron in any amount of time, under those conditions, so the only way that the sample could be nickel-iron now unless it was nickel-iron when it was kicked up into the crust. And since nickel-iron will not break down if it is protected from water and air the way core material is protected, the fact that the core was nickel-iron then means that it is nickel-iron now. (Anaya's fallacy is red herring because she is talking about something that really doesn't matter. The key facts here are that nothing turns into nickel iron, and nickel-iron is stable under core conditions.)

9. A "sample."
10. The "population."
11. The "feature" or the "variable."
12. "Representative."
13. "Unrepresentative."
14. No.
15. No.
16. No.
17. Yes, of course.
18. Yes, of course.
19. Yes, and often is a better sample than a random sample.
20. No and no. It depends on the structure of the population.
21. No and no. It depends on the rate at which the population is likely to change.
22. Yes.
23. Yes.
24. Hasty generalization is a problem with the way a sampling argument was constructed. Red herring is attacking a sampling argument on the basis of something that isn't really a problem.
25. Saying the sample size is too small when it is actually adequate for the method used and the structure of the population. Saying the sample is too old when we have no reason to think that the sample or the population has changed since the sample was taken. Saying that the argument is bad because the sample is not random when the method used is actually appropriate for this particular population structure.
26. The sample size can be too small for the number of values possible for the given variable. The sample could have been taken long enough ago that either the population or the sample could easily have changed in the meantime. The sample could have been taken by method that is not independent of the feature.
27. A sampling method is dependent when members of the population that have the feature are more or less likely to be included in the sample than members of the population that do not have the feature. A sample is only independent member of the population with the feature is exactly as likely to be included in the sample as a member of the population without the feature.
28. The only kind of "bias" that is ever a problem is when the sampling method is dependent. Other things that are called "bias" are not a problem.

For more practice, you can download and do the practice/makeup exercises. (Make sure the document margins are set to 0.5 inches or narrower.)

Copyright © 2010 by Martin C. Young

This Site is Proudly Hosted By.