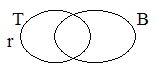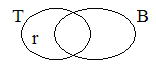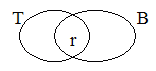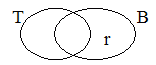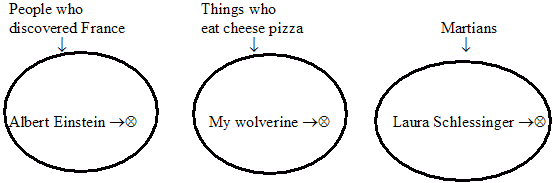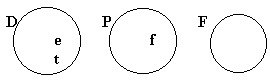Although I'm having you treat every argument you can't otherwise identify
as a deductive argument, "deductive" arguments are actually a very
specific kind of argument, precisely defined and beloved by logic geeks
everywhere. So, if you'll forgive a little bit of geekery, here's the
skinny on deductive arguments.
A deductive argument is one that relies on the purported truth of its
premises and on the purported fact that it is impossible for
those premises to be true if the conclusion is false. (Any argument that
isn't "deductive" is "inductive.")
A deductive argument that has good logical form is called "valid,"
one that doesn't is called "invalid." Invalid deductive
arguments are no good. Pshaw! They're crap. (And they know it, the
stinkers.) By the way, this is something that only applies to
arguments. Only arguments can be valid or invalid. Statements
can be true or false, but they can't be valid or
invalid.
A valid deductive argument with true
premises is called "sound." A sound
argument has a true conclusion. Period. If it's sound,
it's conclusion is true. Not, "most likely," not "really
really probable." Just plain flat true! (Of course, for this to work we
have to be absolutely sure those premises are true.)
Validity: The Easy Part
Before I get into the easy part of validity, I'm just going
to mention, but not test you on yet, the real, correct and true
definition of "validity". Here it is: (Accept no substitutes.)
An argument is valid if, and only if it is impossible
for there to be a situation in which all it's premises are TRUE
and it's conclusion is FALSE.
Scared? Confused? I don't blame you. Many, many, many people have a
very hard time understanding this definition, so I'm reserving the hard
bits for the next chapter. This means you don't have to deal with the
full definition of validity until then. For now, I'm giving you a
simplified rule for validity to get you through this chapter
The Easy Implication of Validity
The correct definition has three logical implications. Two of those
implications are weird and hard to understand, but one is pretty
straightforward, so we'll deal with the easy implication first and leave
the other two for the next chapter.
Easy Implication: If the argument is such that it's
premises, if true, logically force the conclusion to be true, then
the argument is valid.
You could also say this as "an argument is valid if the premises make
the conclusion true" or "if you can't make the conclusion false
without also making at least one premise false, then
the argument is valid" or "if the premises, taken all together, force
the conclusion to be true, the argument is valid."
Now I want to point out an Important and Ansolutely True Fact. The
following statements are all FALSE
- If an argument is valid, then the argument is
such that it's premises, if true, logically force the conclusion to
be true. (False!)
- If an argument is valid, the premises make the
conclusion true. (False!)
- If an argument is valid, you can't make the
conclusion false without also making at least
one premise false. (False!)
- If an argument is valid, the premises, taken
all together, force the conclusion to be true. (False!)
This is because the premises making the conclusion true is a sufficient
condition for the argument to be valid, but is absolutely not a necessary
condition for the argument to be valid. We will talk about the other
ducks, I mean the other ways of making an argument valid in the next
chapter.
How to Think About Validity
The correct way to think about this is to think about assumptions
and possibilities. When you look at one of the
arguments given in this chapter say to yourself, "now, if I assume
that all these premises are true, is it possible
for this conclusion to be false?" (This test works for
all the arguments in this chapter. Other kinds of valid arguments will
be dealt with later)
The definition I'm giving here is sufficient for an argument
to be valid. But it's only one of the ways an argument can be valid, so
it's not a necessary condition for an argument to be valid.
When checking arguments for validity, assume that all the premises are
true, then ask yourself if it is now possible for the
conclusion to be false. If the answer is "yes," the argument is invalid
(wonky). If it's "no," the argument is valid. (No, I
didn't get it mixed up. That's the rule.)
Now possible for conclusion to be false = invalid (wonky)
Now impossible for conclusion to be false = Valid
For instance, the following arguments are all completely invalid
(wonky).
Paris is in France
Berlin is in Germany
Compton is in America |
Cats are mammals
Dogs are mammals
Ferrets are mammals |
People have two legs
Mammals have four legs
Insects have six legs |
Dumbledore is a wizard
Gandalf is a wizard
Merlin is a wizard |
Example 1
If George
Washington had been poisoned, shot, beheaded and then burned to
ashes by his wife for his constant adultery, he would now be dead.
George was not poisoned, shot, beheaded and then burned to ashes
by Martha (pity), so he's not dead.
1.
If Martha Washington had gone absolutely postal on George's
ass, he would be dead.
2. Martha was strictly non-postal.
C. George ain't dead.
If these premises were true, would it be possible for the
conclusion to be false. Absolutely! George could have died from
some other cause, say a bad cold caught when avoiding the irate
father of a young woman he had seduced, so it's logically
possible for the sentence "George ain't dead" to be false, even
if we assume the truth of the premises. So it's invalid
(wonky).
Example 2
If
carnivorous faerie-pixies had sprinkled their magic barbeque
sauce on Ghengis Khan, ol' Ghengis would now be a used car
salesman working out of Bakersfield with an unhappy wife, two
overweight children and a suspicious rash. Well, carnivorous
faerie-pixies did sprinkle magic barbeque sauce on ol'
Ghengis, so Ghengis Khan has a rash and so on.
1. If pixies had
BBQ sauced Ghengis Khan, Ghengis would be a rash-infested
used car salesman working out of Bakersfield.
2. Pixies did BBQ sauce Ghengis Khan.
C. Ghengis does have a rash.
Now, to check validity, we suspend disbelief on the
premises and assume that they're true. So
if we assume magic barbecue sauce exists and will
have these effects when sprinkled, then Ghengis Khan will
be in Bakersfield and so on. One of the effects of the sauce
is a suspicious rash so, given the truth of the
premises, the statement "Ghengis Khan has a rash" can't be
false. So this argument is valid. That's
right, VALID!
Example 3
You
know that big black and white swimming thing they have down
at Seaworld, They call it "Shamu," and it's either a cat or
a dog. Well, it's certainly not a dog, so it must be a cat.
Shamu is either a
cat or a dog
Shamu is not a dog
Shamu is a cat.
Remember again that validity has nothing to do with whether
or not the premises are true. What it depends on whether the
conclusion could be false, if, the
premises were true. Now, if these premises were
true, could the conclusion be false? It couldn't, so this
argument is valid.
Now check these arguments for validity.
All
monkeys are primates. George is a monkey, so it follows
that George is also a primate. Answer
All
monkeys are primates. Pam is a primate, so it follows that
Pam is also a monkey. Answer
All
monkeys are primates. Nick is not a monkey, so it follows
that Nick is not a primate. Answer
All
monkeys are primates. Oswald is not a primate, so Oswald
is not a monkey. Answer
Remember, the actual truth or falsity of the
premises is irrelevant, completely
irrelevant, to the validity of the
argument. Validity is just about the logical
relationship between the parts of the argument, nothing
else.
Logical Form and Validity
Now, some deductive logical forms are
so common, and so important, that they get their own
names. Here's five of them.
Modus Ponens
If X is true,
then Y is true. If
Babe is a shoat, then Joe is a Mocklin
If Roy is a tramp,
then Roy is a bum
X is true
Babe
is a shoat
Roy
is a
tramp
Y is
true Joe
is a
Mocklin Roy
is a bum
Affirming the Consequent
If X is true,
then Y is true. If Babe is
a shoat, then Joe is a Mocklin
If Roy
is a tramp, then Roy is a bum
Y is true
Joe
is a
Mocklin
Roy is a
bum
X is
true
Babe is a
shoat Roy
is a tramp
Denying the Antecedent
If X is true,
then Y is true. If Babe is a
shoat, then Joe is a Mocklin
If Roy is a
tramp, then Roy is a bum
X is not true
Babe
is not a
shoat Roy
is not a
tramp
Y is not
true
Joe is not a
Mocklin Roy
is not a bum
Modus Tollens
If X is true,
then Y is true. If Babe is a shoat,
then Joe is a Mocklin
If Roy is a tramp,
then Roy is a bum
Y is not true
Joe
is not a
Mocklin Roy
is not a
bum
X is not
true Babe
is not a
shoat
Roy is not a
tramp
Disjunctive Syllogism
Either X is true or Y is
true. Either Babe is a shoat or Joe is
a Mocklin Roy is either a
bum or
a tramp
Y is not true
Joe
is not a
Mocklin Roy
is not a
bum
X is
true
Babe is a
shoat
Roy
is a
tramp
In each of the above groups, the first argument is the
general statement of the form, the second is a specific
instance of the form, and the third argument is an
instance of a special case of the form that is easier to
deal with in pictures.
Which ones are valid? Which ones are not? Well, to figure
that out for the first four, you have to make sure that
you understand that "if Babe is a shoat, then Joe is a
Mocklin" just means that "if Babe is a shoat,
then Joe is a Mocklin." It does not go on and
say "if Joe is a Mocklin, then Babe is a shoat." That
particular claim is not a part of any
of these arguments. Because the second claim is not
made or implied by "if Babe is a shoat, then Joe is a
Mocklin," the only way "if Babe is a shoat, then
Joe is a Mocklin," can be false is if Babe is
a shoat but Joe is not a Mocklin. (This is
because it's an "if-then" statement.) It doesn't
say that Babe is a shoat, and it doesn't
say that Joe is a Mocklin. It just says that if
Babe is a shoat, then Joe is a Mocklin.
Too complicated? Well, then we'll go with an easier
example. I've got these special case Roy tramp/Roy bum
arguments which can be easily done in pictures,
and which will hopefully make the difference clear. As
before, the only way that "if Roy is a tramp,
then Roy is a bum" can be false is if Roy is a
tramp, and Roy is not a bum. Under all other
circumstances that statement will be true.
Here's the same point in pictures. Only one of
the following pictures makes "if Roy is a tramp, then Roy
is a bum" false. All the other pictures make it true.
Picture 1
Picture 2
Picture 3
Picture 4
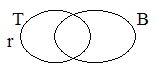
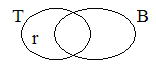
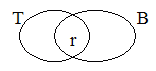
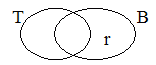
Roy is neither a tramp nor a bum.
Roy is a tramp
but not a bum.
Roy is a tramp
and a bum.
Roy is not a tramp but is a bum.
Well, notice that in picture 2 Roy is a tramp
but is not a bum. That couldn't be true if "if
Roy is a tramp, then Roy is a bum" was true, so picture 2
makes "if Roy is a tramp, then Roy is a bum" false. All
of the other pictures are logically compatible with "if
Roy is a tramp, then Roy is a bum" because they could be
true even if "if Roy is a tramp, then Roy is a bum" was
true. So none of the other pictures makes "if Roy
is a tramp, then Roy is a bum" false.
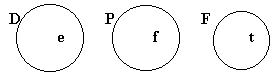
Now, there's an easier way to convey this information
with pictures. We can draw a picture in which putting the
"r" in the "T" circle means also putting it in
the "B" circle. This is easy, because all we have to do is
draw the T circle inside the B circle. Like so:
Picture 5
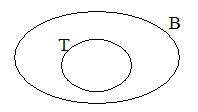
(This actually says "all tramps are bums," which is a
little stronger than "if Roy is a tramp, then Roy is a
bum," but I'm not going to worry about that here.)
Now copy out the above picture four times, and take each
of the following forms in turn, and try to draw in an "r"
to make the premises of that form true, and the
conclusion false. (Picture five, as it stands,
already makes the first premise of each form true. You
just have to make the conclusion false while leaving the
second premise true.) Click on the name of the form to
check your answer.
Modus Ponens
Affirming
the Consequent
If Roy is a
tramp, then Roy is a
bum If
Roy is a tramp, then Roy is a bum
Roy is a
tramp Roy
is a
bum
Roy is a
bum Roy
is a tramp
Denying the Antecedent
Modus
Tollens
If Roy is a
tramp, then Roy is a bum
If
Roy is a tramp, then Roy is a bum
Roy
is not a
tramp Roy is not a
bum
Roy is not a
bum Roy
is not a tramp
Okay, so now you've figured out that affirming
the consequent and denying the
antecedent are invalid. (They are actually
our first two deductive fallacies, because they are
argument forms that look sort of like good forms, but
which are really terrible.) The most interesting one is
the valid form modus tollens,
which is one that many people don't expect to be valid.
(And lots of people take a while to figure out why
it's valid.) Nevertheless, it's an important and
interesting form, especially since it gives us one of
our ways of proving a negative statement.
Think about it, if we can prove that if Roy was a
tramp, then he would be a bum, and we could
also prove that Roy isn't a bum, then that's
enough to prove that Roy isn't a tramp either. If it's
true that if Roy was a tramp, then he would be a bum, is
is it possible for him to be a tramp without
also being a bum? No it isn't, so the fact of his not
being a bum would then prove adsolutely that he was not
a tramp.
More on Disjunctive Syllogism
We've seen the fallacy of "false choice," where an arguer
illegitimately claims that the number of possibilities is
less than it really is. But what about real
choices? What about when there really are only
two possibities? If that is really the case, and
you can eliminate one of the only two possibities, well
then you can apply the valid argument
form of "disjunctive syllogism" and get a sound argument.
1. George is either alive or dead.
2. George isn't dead.
C. George is alive.
Now here's the tricky bit. The paragraph above leaves out
one little detail. We have to be careful not to confuse
the concepts of fallacy and validity.
False Choice isn't a fallacy because of invalidity. It's
actually a perfectly valid disjunctive syllogism
in form. The only thing that makes false choice a fallacy
is that the crucial premise, the one that limits our
choices, is false. Look at the following
argument.
1.
Shamu is either a cat or a dog
2. Shamu is not a dog
C. Shamu is a cat.
Notice now that both arguments have the same valid
form. The second argument only fails because
the first premise is false. Dog and cat are not the only
two possibilities for Shamu's species.
Now let's look at disjunctive syllogism through pictures
and the following argument.
Roy is either
a bum or a tramp
Roy is not a
bum
Roy is a tramp
Now, it's important to know that in logic, the word
"or" is always taken to mean that it could be one and it
also could be the other. You are not
supposed to add the "and not both" that many people
mentally add when they say "or." In logic, "or" should
alsways be understood as saying, "one or the other, or
both." The following three pictures therefore all
make "Roy is either a bum or a tramp" true.
Picture 2
Picture 3
Picture 4
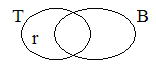
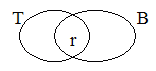
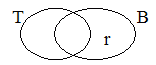
Roy is a tramp but not a bum.
Roy is a tramp
and a bum.
Roy is not a tramp but is a bum.
If Roy is a tramp but not a bum, then the statement
"Roy is either a bum or a tramp" is true.
If Roy is a tramp and a bum, then the statement "Roy is
either a bum or a tramp" is true.
And if Roy is not a tramp but is a bum, then the
statement "Roy is either a bum or a tramp" is
true..
Now, out of those three pictures above, which one also
makes the statement "Roy is not a bum" true? It's
picture 2, isn't it?
Picture 2
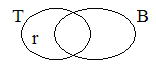
Roy is a tramp but not a bum.
Now, this is the only picture that makes both
of the premises true.Does it make the
conclusion true? If it does, the argument form is valid.
Terminology (Again)
Remember, a logically good deductive
argument is called valid, and a valid
argument with true premises is called sound.
A logically good inductive argument is
called strong, and a strong argument with
true premises is called cogent.
The words "valid" and "sound" are not used
for inductive arguments, and the words
"strong" and "cogent" are not used for deductive
arguments.
#########################################################
This chapter concerns the correct defininition
of "validity," which is the one part of logic that
most people get wrong most often. I'm not saying it is
a hard thing to learn. It's certainly not a complicated
thing. BUT, it's something that many people find very
counterintuitive. ("Counterintuitive" means that it's
very different from what you want to think it is.),
Beacuse it's so counterintuitive, many people have a
strong tendency to instinctively reject the
correct defininition of validity in favor of an incorrect
definition that feels right but which is
completely and utterly wrong. So if you read
the definition of validity in this chapter and find
yourself saying "that can't be right, he must
mean something different from what he's saying,"
get a grip on yourself and understand that the
definition of validity I will give here, as weird as
it seems, is the only correct definition.
But don't be scared! I'm not saying the definition
will be difficult, I'm just saying that it
will be weird.
If you're willing to accept something as weird-but-true,
then you will definitely be able to master the
definition of validity.
Validity Explained Fully
In the previous chapter I gave you a rule for
determining validity that was good for some
valid arguments, but not for all valid
arguments. Now I'm going to give you the real
definition of validity. some of you won't like it, some
of you will want to reject it, but it's the only game in
town, so you'd better accept it.
Okay, here's where it gets weird. Remember, you'll be
okay if you read the definition of validity very
carefully, and interpret it absolutely
literally.
By the way, this is something that only
applies to deductive arguments. Only
deductive arguments can be valid or invalid. Statements
can be true or false, but they can't
be valid or invalid.
A deductive argument is one that relies on the
purported truth of its premises and on the
purported fact that it is impossible for those premises
to be true if the conclusion is false. (Any argument
that isn't "deductive" is "inductive.")
A deductive argument that has good logical form is
called "valid," one that doesn't is
called "invalid." Invalid deductive
arguments are no good. Pshaw! They're crap. (And they
know it, the stinkers.)
A valid deductive argument with true
premises is called "sound." A sound
argument has a true conclusion.
Period. If it's sound, it's conclusion is true.
Not, "most likely," not "really really probable." Just
plain flat true! (Of course, for this to work we have to
be absolutely sure those premises are true.)
An argument is valid if, and only if
it is impossible for there to be a situation
in which all it's premises are TRUE and it's conclusion
is FALSE.
You probably didn't get that the first time, so go back
and read it again. I'll wait.
Did you get it? We'll see. Answer the following
"true/false" quiz.
1. An argument where it's possible to
have all true premises and a true
conclusion all at the same time is always valid.
Answer
2. An argument where it's impossible
to have all true premises and a true
conclusion all at the same time is always valid.
Answer
3. An argument where it's possible to
have all true premises and a false
conclusion all at the same time is always invalid
(wonky). Answer
4. An argument where it's impossible
to have all true premises and a false
conclusion all at the same time is always invalid
(wonky). Answer
5. An argument where it's possible to
have all true premises and a false
conclusion all at the same time is always valid.
Answer
6. An argument where it's impossible
to have all true premises and a false
conclusion all at the same time is always valid.
Answer
So if you're trying to check the validity of an
argument, and you figure out a way that the premises
and conclusion can all be true, then you haven't
checked the validity of that argument. You gotta try
to figure a way to make the premises true
and the conclusion false. If that can't
be done, the argument is valid. If it can be done,
then it's invalid (wonky).
In deductive logic, we interpret the word "and" in
a very special way. We interpret as meaning "both of
these are true". What? Well, okay, it's not that
special. But we do have a special name for
statements made up of two other statements joined by
"and". We call such sentences "conjunctions". Yeah,
"conjunctions". The important thing here is that, in
deductive logic "roses are red and violets are blue"
is only true if it is that case that both
halves of the phrase are true. So if roses are not
red the conjunction "roses are red and violets are
blue" is false, and if "violets are not blue", the
conjuction "roses are red and violets are blue" is
false, aaaaand if roses are not red and
violets are not blue, the conjunction "roses are red
and violets are blue" is . . . . . . false.
Roses
are red.
Violets are blue .
Roses are red or violets are blue.
Roses
are red.
Roses are red or violets are blue.
Violets are blue .
Roses are red or violets are blue.
And the following are all invalid:
Roses
are red or violets are blue.
Roses are red.
Roses are red or violets are blue.
Violets are blue.
Cheese is yellow or goop is green.
Roses are red or violets are blue.
Violets are blue or cheese is yellow.
Goop
is green.
Roses are red or violets are blue.
Violets are blue or cheese is yellow.
Cheese
is yellow or goop is green.
Roses are red or violets are blue.
Violets are blue or goop is green.
To
check that the green arguments are
valid, try to come up with a situation in which
the premises of the arguments are all true and
the conclusion is false. If you can't,
the argument is valid.
To check that the red arguments are invalid,
try to come up with a situation in which the
premises of the arguments are all true and
the conclusion is false. If you can, the
argument is invalid.
NOT
Remember the valid argument form of Modus
Tollens
If
X is true, then Y is true.
If Babe is a shoat, then Joe
is a Mocklin
If Roy is
a tramp, then Roy is a bum
Y is not true
Joe
is not a
Mocklin Roy
is not a
bum
X is not
true Babe
is not a
shoat
Roy is not a tramp
And the invalid argument
form of Denying the Antecedent
If X
is true, then Y is true.
If Babe is a shoat,
then Joe is a Mocklin
If
Roy is a tramp, then Roy is a bum
X is not true
Babe
is not a
shoat Roy
is not a
tramp
Y is not
true
Joe is not a
Mocklin Roy
is not a bum
And when we combine "or" and "not", we get the
valid form of Disjunctive Syllogism
Either
X is true or Y is true.
Either Babe is a shoat or
Joe is a Mocklin Roy is
either a bum
or
a
tramp
Y is not true
Joe
is not a
Mocklin Roy
is not a
bum
X is
true
Babe is a
shoat
Roy
is a tramp
When we combine "and", "or" and "not", we
get all kinds of interesting arguments. (Well, you
could at least act like they're
interesting.)
The following arguments are all valid:
Roses
are red.
Violets are blue .
Roses are not red or violets are blue.
Roses
are not red.
Roses are not red or violets are blue.
Violets are not blue .
Roses are red or violets are not blue.
Roses
are red and violets are not blue.
Roses are red.
Roses are not red and violets are blue.
Violets are blue.
Roses are not red.
Violets are not blue .
Roses are not red and violets are not blue.
Roses
are not red
Roses
are red or violets are blue.
Violets
are blue.
Violets
are not blue.
Roses
are red or violets are blue.
Roses are red.
Roses
are not red and cheese is not yellow.
Cheese
is yellow or goop is green.
Roses are red or violets are blue.
Violets are blue and goop is green.
Roses
are not red or cheese is not yellow.
Cheese
is yellow or goop is green.
Roses are red or violets are blue.
Violets are blue or goop is green.
Cheese
is not yellow or goop is green.
Roses
are red or cheese is yellow
Roses are not red or violets are blue.
Violets are blue or goop is green.
And
the following are all invalid:
Roses
are not red and violets are not blue.
Roses are red and violets are blue.
Roses
are not red and violets are not blue.
Roses are red or violets are blue.
Roses
are not red or violets are not blue.
Roses are red and violets are blue.
Roses
are not red or violets are not blue.
Roses are red or violets are blue.
Roses
are not red.
Roses are red or violets are blue.
Roses are not red or violets are not blue.
Roses are red.
Cheese
is not yellow or goop is not green.
Roses are not red or violets are not blue.
Violets are not blue or cheese is not yellow.
Roses
are not red and cheese is not yellow.
Roses
are red or violets are blue.
Violets are blue and goop is green.
Roses
are not red or cheese is not yellow.
Roses
are red or violets are blue.
Violets are blue or goop is green.
Cheese
is not yellow or goop is green.
Roses are not red or violets are blue.
Violets are blue or goop is green.
Cheese
is not yellow or violets are not blue
Cheese is yellow or goop is green.
Roses are red or violets are blue.
Roses are red and goop is green.
To check that the green arguments are
valid, try to come up with a situation in which
the premises of the arguments are all true and
the conclusion is false. If you can't,
the argument is valid.
To check that the red arguments are invalid,
try to come up with a situation in which the
premises of the arguments are all true and
the conclusion is false. If you can, the
argument is invalid.
Tautologies and Contradictions
A "tautology" is a statement that can't be false.
Here an example:
Roses
are red or roses are
not red.
Given that this statement is a disjunction, it
follows that if either side is true, the
disjunction will be true. So, if roses are red,
the statement is true and if roses are
not red, the statement is still true.
A "contradiction" is a statement that can't be
true. Here an example:
Roses
are red and roses are not red.
Given that this statement is a conjunction, it
follows that if either side is false,
the conjunction will be false. So, if roses are
red, the conjunction is false because
the other half will be false and
if roses are not red, the statement is still
false because in that case, the first
half will be false.
Oh, and there's pairs of statements that can't
both be true, like:
1. Roses are red.
2. Roses are not red.
Whichever way you cut it, one of these
statements is false.
And Now the Weirdness Begins
Remember that the correct definition of
validity is that an
argument is valid if and only if it is
impossible to have a situation in which the
premises are true and the conclusion is false.
Let's call that situation "Situation S".
In "Situation S" an argument is such that its premises are true AND
its conclusion is false.
Catch that word "and".
Now remember, an argument is
valid if and only if it is impossible
to have a situation in which the premises are
true and the conclusion is false. To put
it another way, an argument is
valid if and only if Situation S is impossible
for that argument. In yet other words, Situation S
being impossible is both a necessary and a
sufficient condition for the argument being valid.
(And Situation S being impossible is both a
necessary and a sufficient condition for the
argument being valid.)
Let me say that again, if Situation S is impossible
the argument is valid.
And if Situation S is possible the
argument is invalid.
So what kinds of things make Situation S
impossible?
Well, Situation S has two parts. First,
all the premises are true, and
second, the conclusion is false.
Let's call these Part 1 and Part 2. To recap:
Situation S: Premises are all true and the
conclusion is false.
Part 1: Premises are all true..
Part 2: Conclusion is false.
Now remember the difference between necessary and
sufficient conditions. This means:
Situation S is sufficient for Part 1.
Situation S is sufficient for Part 2.
Part 1 is necessary for Situation S.
Part 2 is necessary for Situation S.
What this means that is, if Situation S
is possible, then both Part 1 and Part
2 have to be possible.
From that it follows that, if Part 1 is
impossible, then Situation S is
impossible and, if Part 2 is impossible,
then Situation S is impossible, which
means that if either Part 1 or
Part 2 is impossible, then Situation S
is impossible.
Now, here's a question:
If Part 1 is impossible and Part 2 is possible,
is Situation S possible?
Remember that both parts are necessary
for Situation S, so if Part 1 is impossible, it
follows that Situation S is impossible too.
Okay, if that didn't make sense, let's try the
same question without the abstractions:
If premises all true is impossible
and conclusion false is possible, it
follows that the conjunction (remember
that word) the conjunction premises all true
and conclusion false is also
impossible. And if premises all true and
conclusion false is impossible,
the argument is valid.
Also:
If premises all true is possible but
conclusion false is impossible, it follows
that the conjunction (remember that
word) the conjunction premises all true and
conclusion false is also
impossible. And if premises all true and
conclusion false is impossible,
the argument is valid.
So, from this two weird things follow:
If an argument is such that it is impossible
for all the premises to be true,
it follows that the argument is valid,
no matter what the conclusion is.
And:
If an argument is such that it is impossible
for the conclusion to be false, it
follows that the argument is valid,
no matter what the premises are. .
That's the weirdness. (And if that sounds normal
to you, you might be a nerd.)
Now, here's a question you probably haven't
thought about. But you'd better think about it,
because if you answered it without thinking, you'd
almost certainly get it wrong.
Do the premises have to make
the conclusion true in order for the argument to
be valid?
No they don't. One common, but misleading,
definition of validity is that "an argument is
valid if and only if the premises, if true, make
the conclusion true." This is misleading because
we can have valid arguments in which the preimises
have no logical relationship to the
conclusion. For instance, if the conclusion is a
"tautology," which is a statement that cannot be
false, the argument will be valid no matter what
the premises are! Let me emphasize that.
| An argument with a
conclusion that can't
be false IS necessarily
valid. |
Consider the following argument:
George
Bush is over 1,000 feet tall.
The universe is secretly ruled by a small
fish living under your couch.
Chocolate either is or is not made from crude
oil.
Now ask yourself, can we have a situation where
all those premises are true and the
conclusion is false? Sure those premises
(logically) could be true, but can that
conclusion ever be false? If chocolate
is made from crude oil, the conclusion is true. If
chocolate is not made from crude oil,
the conclusion is still true. And if we don't know
what chocolate is made from, it still either is or
is not crude oil, so the conclusion has got
to be true! This conclusion therefore can't be
false, and we know the argument is valid whatever
the premises are! So that argument just above this
paragraph is valid, and so is this one!
All
wombats are bitter mysogynists living in dank
warrens under the boulevard cafes of Paris.
Cigarette smoking makes you cool, especially
if you cough up a diseased lung right in front
of the Pope.
It may or may not be true that Osama Bin Laden
is posing as a cab driver in Des Moines, Iowa.
You think that's weird? Well check this
out.
| An argument with premises
that can't all be true
IS necessarily valid. |
Read that again. It says that if the
premises can't all be true, then the
argument is valid. It doesn't even mention
the conclusion, which means that an argument with a
false, stupid or impossible conclusion can be
perfectly valid, provided it has premises that
somehow contradict each other.
I'll say it again. If an argument has mutually
contradictory premises, that is, premises
which contradict each other, then that argument is
automatically valid.
Test yourself. Which of the following two
sentences says the same thing as the sentence
underlined above?
A. An argument with
premises that can't all be true is necessarily valid.
B. An argument with
premises that can't all be true is necessarily invalid
(wonky).
If you said "A," you're right!
If you said "B," you're wrong.
Here's an example of an argument that's valid
because of contradictory premises.
Elvis is
dead.
Elvis is alive.
Laura Schlessinger is a woolly mammoth. |
De
~De
Wl VALID!! |
Think about it. Is it possible to have a
situation in which the premises are true and the
conclusion is false? Sure, it's possible to have a
situation in which the conclusion is
false, but for the argument to be invalid (wonky),
it has to be possible for the premises to all
be true at the same time the conclusion is false.
So if the premises can't all be true, the argument
is valid. (If you still think the argument
is invalid (wonky), draw a picture in which the
premises are all true and the conclusion is false.
Remember, there's only one Elvis, and you can't be
both dead and alive.)
Is this a startling concept? Well, remember that
logic is startlingly different from the way people
usually think, and from the way they expect you
to think.
Now, here's the weirdest thing of all. The
following argument is VALID.
That's right, valid. Brace yourself,
because this valid argument is
going to seem totally weird to you!
Cheese is a mineral.
Cheese is not a mineral
Elvis is both alive and not alive.
Remember, this is VALID. (Weird, huh?) You will
of course notice that the conclusion cannot
possibly be true. It's a logical
self-contradiction! You can't both be and not be
anything! The thing to remember here that having a
conclusion that can't be true doesn't necessarily
make an argument invalid. If the premises
contradict each other, the argument is valid, no
matter what the conclusion is!
Test yourself: Does the fact that we can make a
valid argument for absolutely any
conclusion mean that logic can prove absolutely anything?
Answer
To put it another way, can you construct a sound
argument for a false conclusion? Answer
Terminology
Logic requires a very precise use of terminology.
So here it is. A logically good deductive
argument is called valid, and a valid
argument with true premises is called sound.
A logically good inductive argument is
called strong, and a strong argument
with true premises is called cogent.
The words "valid" and "sound" are not
used for inductive arguments, and the
words "strong" and "cogent" are not used
for deductive arguments.
The validity test is as
follows:
First, assume that the argument's conclusion is
false.
Second, ask yourself if it’s now possible for the
all the premises to be true. (Sometimes assuming
the conclusion false will make a premise false.
Other times there will be another reason why the
premises can’t all be true.)
If it’s possible for all the premises to be true,
even if the conclusion is false, then the argument
is INVALID. (or “wonky.” Remember “possible” =
“wonky.”)
If there is any reason why the premises can’t all
be true, the argument is VALID. Maybe assuming the
conclusion false makes a premise false. Maybe they
simply can’t all be true together. Either way,
“impossible” = “valid.”)
These two exercises are meant to practice your
ability to apply the definition of validity.
A Final Note
If two deductive arguments have the same form, it
is exactly the same form. There won't be
even the slightest formal difference betweene
then. None. No difference in form whatsoever. And
if there is a difference between the forms of two
deductive arguments, they're simply not the same
form at all. The concept of two deductive
arguments having "similar" logical forms
is neither useful nor even meaningful. They either
have the same form or they don't, and if they
don't, the validity of one has nothing to do with
the validity of the other. This property is unique
to deductive arguments. Inductive arguments are
different.
Just to remind you, the following two statements
are absolutely true.
An argument with a conclusion that
can't be false IS necessarily
valid.
An argument with premises that can't
all be true IS necessarily valid.
Practice Quiz.
1. Do most people find the concept of validity
easy to understand?
7. Is this valid or invalid: If the
British had caught and executed Benjamin
Franklin in 1777, Benjamin Franklin would be
dead. Benjamin Franklin is not dead,
so the British did not execute
Benjamin Franklin.
8. Is this valid or invalid: If the
British had caught and executed Benjamin
Franklin in 1777, Benjamin Franklin would be
dead. The British did not execute Benjamin
Franklin, so Benjamin Franklin is not dead.
9. Is this valid or invalid: If the
British had caught and executed Benjamin
Franklin in 1777, Benjamin Franklin would be
dead. The British did execute Benjamin Franklin,
so Benjamin Franklin is dead.
10. Is this valid or invalid: If the
British had caught and executed Benjamin
Franklin in 1777, Benjamin Franklin would be
dead. Benjamin Franklin is dead, so the
British did execute Benjamin Franklin.
11. Is this valid or invalid: Whales
are fish. Whales are not fish. So
cheese is a mineral.
12. Is this valid or invalid: Whales
are mammals. Whales are not fish. So cheese is not
a mineral.
13. Is this valid or invalid: Whales
are mammals. Whales are fish. Fish are never
mammals. So whales are fish.
14. Is this valid or invalid: Whales
are mammals. Fish are never mammals. Whales are
not fish. So some whales eat fish.
19. Does validity depend on whether the premises
of arguments are actually true or false.
20. Is it true that an argument cannot be valid if
the premises and conclusion are false.
21. "An argument is valid if and only if ...... "
Practice Quiz Answers
1. The concept of "validity" is very
counterintuitive and most people find it very
difficult to master.
8. Invalid
9. Valid
10. Invalid
11. Valid. Yes, valid. That's right, it's valid.
12. Invalid
13. Valid. Think about it. Can the premises all
be true? If they can't, the argument is valid.
14. Invalid. Yep, invalid.
15. Deductive.
16. Inductive.
17. Deductive.
18. Inductive.
19. Nope. Validity has nothing to do with the
actual truth or falsity of the premises of an
argument.
20. Nope. An argument can be valid even
if all the premises and conclusion are
false.
21. "An argument is valid if and only if it is
impossible for there to be a situation in which
all its premises are true and it's conclusion is
false.
Copyright © 2011 by Martin C. Young