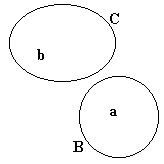
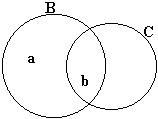
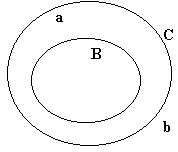
~Ba = ?
~Bb = ?
~Ca = ?
~Cb = ?
 |
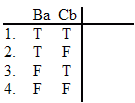
~Ba = ? ~Bb = ? ~Ca = ? ~Cb = ? |

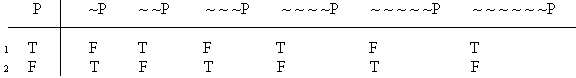
 |
|
||||||||
 |
|
||||||||
 |
|
 |
 |
 |
 |
|
||||||||
 |
|
||||||||
 |
|
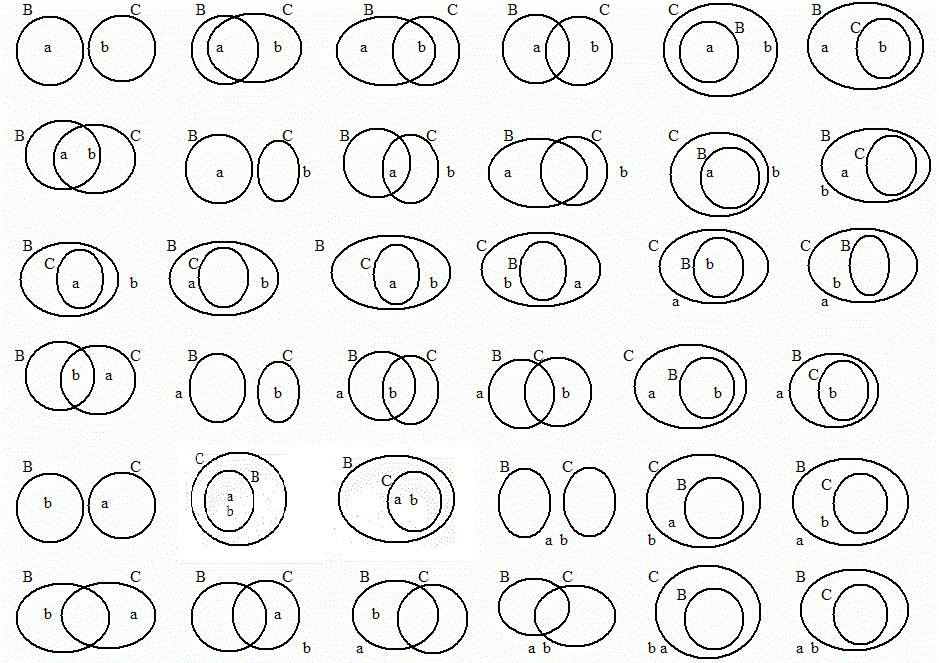
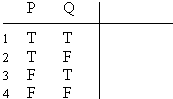
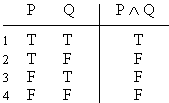
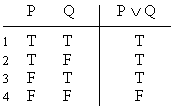
Practice 2. Use your own paper or the answer sheet at not homework. Write down or fill in the values indicated. (Hint: Looking at the relevant truth tables may be helpful.)
|
