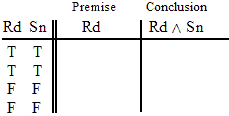
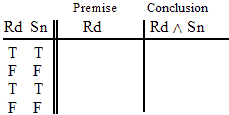
~Nu
Ga ^ Ki
Me
Fa ^ Me
Lo
Lo v Gi
~Jo
Jo
Ko
Ku
Je
Mo v Je
Fi
Fe v Fu
Ji
La ^ Ji
~Na
Lu
~Ka
Mi
Go v Li
Go
Le ^ Ii
Le
No v Gu
No
He ^ Ni
He
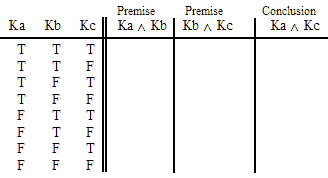
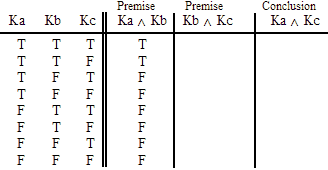
Ge ^ Io
Ja
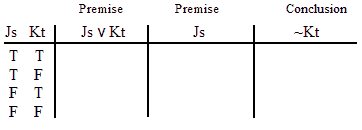
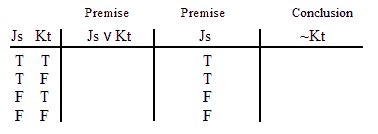
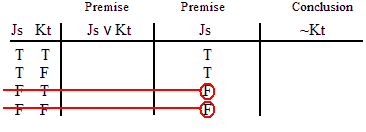
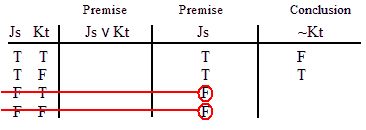
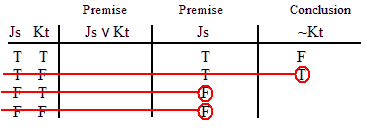
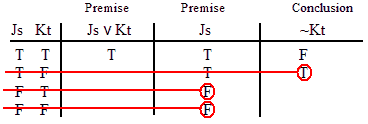
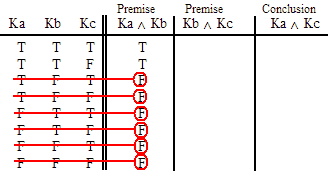
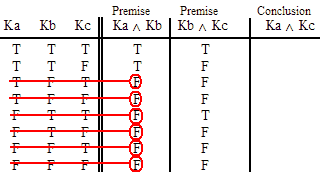
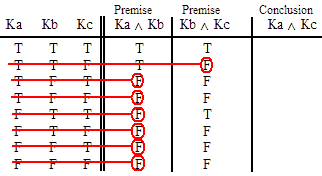
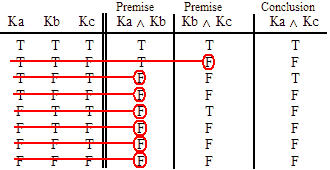
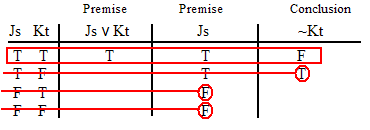 INVALID (by row one.)
INVALID (by row one.)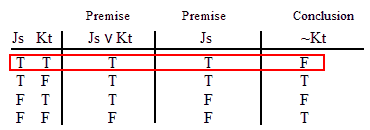
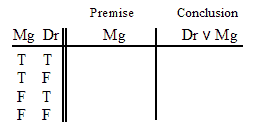
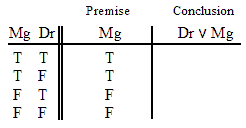
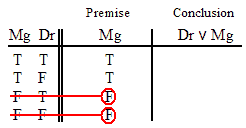
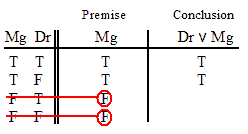
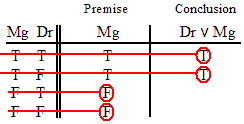 VALID.
VALID.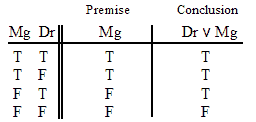
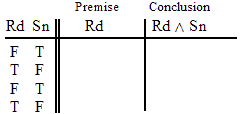
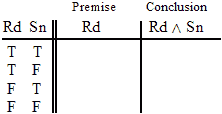

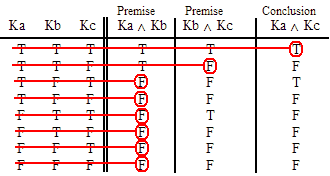
| Nu ~Nu Ga ^ Ki |
Fa Me Fa ^ Me |
Gi Lo Lo v Gi |
~Jo Jo |
Ke Ko Ku |
| Hu Je Mo v Je |
Fo Fi Fe v Fu |
Ma Ji La ^ Ji |
Na v Lu
~Na Lu |
Ka ^ Mi ~Ka Mi |
| Ne v Ha Go v Li Go |
Ho v Ju Le ^ Ii Le |
Ie ^ Hi No v Gu No |
Mu ^ Ia He ^ Ni He |
Iu Ge ^ Io Ja |
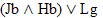 |
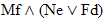 |
 |
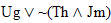 |
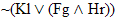 |
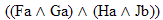 |
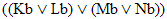 |
Practice 4.
Use your own paper or the answer sheet at practice 04. For each of the following arguments, prove it valid or invalid by truth
table.
|
