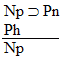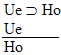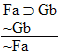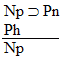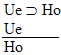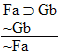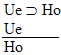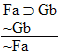Logic Chapter Ten
Next Chapter

Exploiting conditionals in derivations.

Remember that exactly two of the following four arguments are valid. (Take a moment to figure out for yourself which two.)

The two valid arguments can be derived with appropriate rules.



Here's the rule that applies to the first one.

Running Forwards Along A Conditional

size="13">Rule 11. Modus Ponens (Abbreviated by "MP")
If "PQ" and "P" are both available lines, then "Q" may be written as a new line in the derivation.

(Pay close attention to what this rule doesn't say. Notice it doesn't say anything about "PQ" and "Q" being available lines.)

Now, let's derive that first valid argument. 

Here are some more valid arguments. Make sure you try to derive them yourself before clicking on them for the answers.
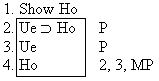
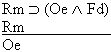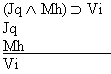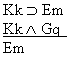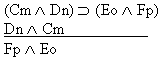Remember that PQ is only false where P is true and Q is false, which means that the only situation in which Q can't be false, is where PQ is true and P is true. Now reverse that. Imagine that we know that PQ is true and Q is false. What does that tell us about P? Well, can P be true in that situation? No it can't, because if Q is false, the only way to make PQ true is to make P false. Which gives us another rule:


Running Backwards Back Along A Conditional

Here's the rule that allows us to derive the second valid argument.

Rule 14. Modus Tollens (Abbreviated by "MT")
If "PQ" and "~Q" are both available lines, then "~P" may be written as a new line in the derivation.

(Again, pay close attention to what the rule doesn't say. Notice it doesn't say anything about "PQ" and "~P" being available lines.)

Now, let's derive that second valid argument. 

Here are some more valid arguments. Make sure you try to derive them yourself before clicking on them for the answers.



Why The Other Two Arguments Ain't Valid.

Remember the two deductive "Fallacies," which are argument forms that look sort of like good forms, but which are really terrible:

Affirming the Consequent occurs when an arguer takes a true "if P then Q" statement and reverses it, treating it as though it said "if Q then P"

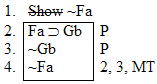
If NASA sent an expedition to Mars and back in 1974 then we'd have Mars rocks on Earth. We do have Mars rocks on Earth. (This is true!) 
So NASA did send an expedition to Mars and back in 1974.
If saboteurs from Luxembourg had planted a nuclear device in Mount Saint Helens, that mountain would have blown up. Mount Saint Helens did blow up, so Luxembourg did sent saboteurs to the US.
If the British had caught and executed Benjamin Franklin in 1777, Benjamin Franklin would be dead. Benjamin Franklin is dead, so the British did catch and execute Benjamin Franklin in 1777.

Denying the Antecedent takes a true "if P then Q" statement and treats it as though it said "if not P then not Q"

If NASA sent an expedition to Mars and back in 1974 then we'd have Mars rocks on Earth. NASA didn't send an expedition to Mars and back in 1974, so there are no Mars rocks on Earth.
If saboteurs from Luxembourg had planted a nuclear device in Mount Saint Helens, that mountain would have blown up. Luxembourg has never sent saboteurs to the US, so Mount Saint Helens has never blown up.
If the British had caught and executed Benjamin Franklin in 1777, Benjamin Franklin would be dead. The British did not catch and execute Benjamin Franklin in 1777, so Benjamin Franklin is not dead.

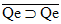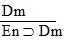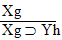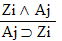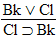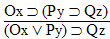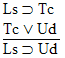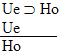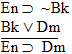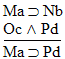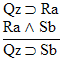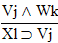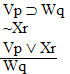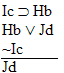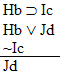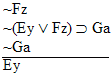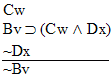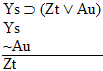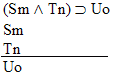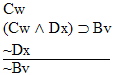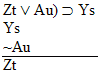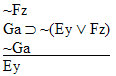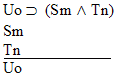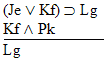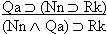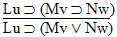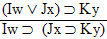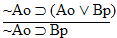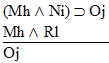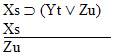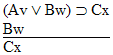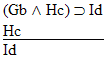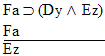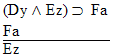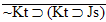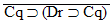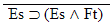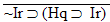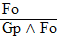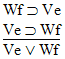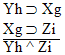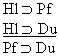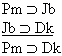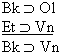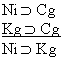As usual, here is a whole s***load of arguments for you to practice on. At least some of the valid ones require conditional proof. Some of them need you to use conditional proof inside a derivation.


Isn't this fun?

Practice 10. Use your own paper or the answer sheet at practice.
This homework requires you to derive at least four arguments.
Circle the valid arguments, and cross out the invalid ones. Derive at least four of the valid ones.
1. 2. 3. 4. 5. 6.
7. 8. 9. 10. 11. 12.
13. 14. 15. 16. 17. 18.
Remember, you gotta do four derivations to complete this assignment.

Copyright © 2007 by Martin C. Young

Next Chapter
This Site is Proudly Hosted By:
WEBster Computing Services