Logic Chapter One

Next Chapter
An easily printable ".rtf" version of this file is available at logic01text.rtf. Make sure your word processor is set to 0.5" (one half-inch) margins.
(I may not be able to make rtfs for all my chapter, so make sure you tell me if the rtf files help you.)

DEDUCTIVE ARGUMENTS

Arguments come in two flavors. There are deductive arguments (covered by this course), which establish the precise logical relationships between ideas, and there are inductive arguments which establish truths about the universe we live in. Deductive arguments can give you certainty, but that certainty only applies to the logical relationships involved. Inductive arguments, (not covered by this course), can prove things about the world, but the price of never giving you absolute certainty. Let me explain.

To tell whether an argument is deductive or inductive, you ignore the question of how the premises are established, and whether or not they are true or false, and focus on the logical form of the argument as it is presented to you. Here is a deductive argument.

All cats are selfish.
Socrates is a cat.
Socrates is selfish.

Assuming that there's nothing wrong with the logical form of this argument, and that the premises are true, it follows that the conclusion is absolutely true. Think about it. If it is true that Socrates is a cat, and that all cats are selfish, could it possibly be true that Socrates is not selfish?

Now, here's an inductive argument.

All cats known to history are selfish.
All cats are selfish.

Again assuming that there's nothing wrong with the logical form of this argument, and that the premise is true, it follows that the conclusion is very very likely, but it does not quite follow that the conclusion is absolutely true. Think about it. If every cat everyone has ever known has been selfish, then wouldn't you strongly tend to think that all cats are selfish? But could you be absolutely sure that there wasn't some cat, unknown to history, that was not selfish?

Can a deductive argument prove something about the world with absolute certainty? No. No argument is ever stronger than its weakest premise. If a deductive argument has a conclusion that's about the world, then it must have a premise that is also about the world. Ultimately, that premise must be justified by observation, by looking at the world. All arguments based upon looking at the world are inductive arguments, so every conclusion about the world, whether it shows up in an inductive or a deductive argument, is ultimately based on some inductive argument. The bottom line is that nothing apart from logical relationships between ideas can be known with certainty. Conclusions about the world always come with at least some uncertainty.

The study of relationships between ideas is called formal logic or, (because it's easier to do with symbols), symbolic logic. In order to get a basic handle on symbolic logic, it's necessary to learn the language. We will learn one language for symbolic logic over the course of this class, starting with schemes.

SCHEMES

A scheme is just a list of symbols together with the meanings we've (temporarily) assigned to them. (It's like a little tiny made-up language.) Here's an example.

                                              Bx : x is a bear
                                              Cx : x is a cat
                                              a : King Arthur
                                              b : Bill Clinton

In this class, we will use upper case letters, A, B, C,.... to stand for properties (call them "predicate letters") and lower case letters to stand for things (call these "object letters"). Object letters come in two flavors. There's "x," "y" and "z" (called "variables") which can stand for just some thing, when we don't know what particular thing it is, or it could be anything, or all things, or nothing. Then there's all the other lower case letters, a, b, c,...., (called "names") which are reserved for particular things. So when you see a variable, you know it means "just any old thing" but when you see a name you know it stands for some particular, unique thing, like you, or me, or Ricky Martin's left big toe, or the planet Neptune or anything, just so long as it's a particular thing. So the scheme above lets us talk about bears in general, and cats in general, without necessarily referring to any particular cats or bears, and to specifically talk about King Arthur and Bill Clinton.

Sometimes, I will use the upper case letters "P," "Q" and "R" to stand for "just any old statement." It's like a variable, only for statements rather than objects.

STATEMENTS

A statement (in deductive logic) is a definite claim that we using whatever scheme we happen to choose. (It's like saying something in a little tiny language.) At the moment, the scheme I gave above allows us to say the following four things: "Ba" which means "King Arthur is a bear," "Bb" which means "Bill Clinton is a bear," "Ca" which means "King Arthur is a cat" and "Cb" which (guess what) means "Bill Clinton is a cat." (These are called "simple" statements. Later on, we'll be able to say more complicated things.)

It's important to form statements in exactly the right way. "Ba" is a proper statement, but "aB" isn't. Nor is "CB," "ba" or "aCb" and so on. Statements that are made the right way are called "well-formed" while those that aren't are called "ill-formed." Make sure all your statements are well formed.

WORLDS

A world is an imaginary universe, or version of the real world, that we make up to try to make statements true or false. There's a couple of ways to represent worlds. The easiest to understand is by diagrams, so I'll start with that.

What this picture means:
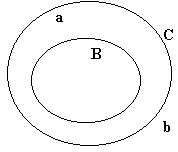
First, if there are any bears at all in this world, they are inside the "B" circle. If there are any cats at all, they are inside the "C" circle.
Second, because the "a" is inside the "B" circle but not the "C" circle, it means that King Arthur is a bear and not a cat.
Finally, because the "b" is inside both circles, it means that Bill Clinton is both a bear and a cat.

It's important to remember that the empty spaces are all places that other objects could be. There could be other objects anywhere in this picture. Thus, this picture doesn't say anything beyond the meaning I just told you about.

VALUE

The value (or "truth value") of a statement just means whether it's true or false in a particular world. Here are the values of the four statements given above in this particular world. (Can you tell why these four statements have the values they do?)
Ba = true, Bb = true, Ca = false, Cb = true.
Notice also that the world specifies more than just the values of these four statements. For instance, it also says that something can be both a bear and a cat.

PRACTICE

What are the values of our four statements in this world?

Ba = ?

Bb = ?

Ca = ?

Cb = ?

(For the answer, rest your cursor on the relevant statement. The answer will appear as a web address at the bottom of your screen. Or click the relevant statement.) By the way, the fact that neither the "b" nor the "c" is inside the "B" circle doesn't mean that the "B" circle is necessarily empty. It might be empty, but there might be something there. This picture doesn't say.

What about this one?

Ba = ?

Bb = ?

Ca = ?

Cb = ?

And finally, this one? (Remember that everything inside the "B" circle is also inside the "C" circle!

Ba = ?

Bb = ?

Ca = ?

Cb = ?

Practice. Use your own paper or the answer sheet at it's not homework. Write down or fill in the values indicated.

	1. Eg = ____ 2. Eh = ____
	3. Jk = ____ 4. Ek = ____ 5. Jg = ____ 6. Jh = ____
	7. Mg = ____ 8. Mh = ____ 9. Mk = ____
	10. En = ____

This Site is Proudly Hosted By: