Logic Chapter Eight

Logic Chapter Eight
Next Chapter

To review, Indirect proof works like this: You assume that the thing you're trying to prove is false and then see if that assumption leads to something that is obviously not true. If you do get an obvious falsehood, you've proved that the thing you assumed to be false is in fact true. Why? Well since it was that original assumption that gave you that obvious falsehood, it follows that the assumption itself is false.

Here's an example. Say you're trying to prove that pigs can't fly. Using indirect proof, you start off by assuming the negation of that claim, which is that they can fly. Then you deduce the logical consequences of that assumption. If pigs could fly, what else would be true? Well, we'd all have to wear hats, and wash our cars more frequently. Buildings would need special devices to prevent pigs from roosting on them. Pig farmers would have to keep pigs in cages and, of course, every so often we would hear someone say "hey, watch out for that flying pig!" Since none of those things is true, we can infer that our original assumption that pigs can fly is false, and so the claim "pigs can't fly" is true.

From the point of view of symbolic logic, the negative assumption doesn't have to lead to any particular obvious falsehood. We just have to come up with some obvious falsehood. Any obvious falsehood will do. The kind of obvious falsehood logicians like the most is the logical contradiction, which means having the same claim be both true and false. Since no claim can be both true and false, there's a falsehood. So, if after assuming that pigs can fly we somehow manage to prove that Mars is and is not made of taco sauce, we will have proved that pigs can't fly, even if there's no obvious connection between pigs, Mars and taco sauce.

So we have the rule:

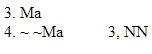
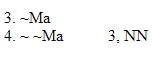
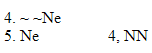
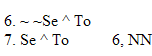
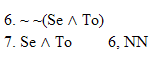
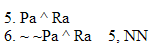
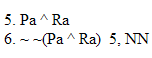
Rule 5. Indirect Proof (This rule has two parts) (Indicated by "IP")

Part One: Whenever you write a show line for any formula, you can write the exact negation of that formula, provided that it is the very next thing you write. (Indicate by writing AIP on that line)

Part Two: If any formula and its negation both appear as available lines in a derivation without an uncancelled "show" between them, then the closest "show" that is above them both may be cancelled, and a box may be drawn around the closest one and any other lines there may be between it and that show line. If the relevant show line is line #1, then the derivation is successfully finished. (Put IP by the "show")
(The first six rules are conveniently listed on Logic Rules Sheet One)

Notice that there's an assumption on the very next line. What you assume is the explicit negation of what you're trying to prove. That is, you take the whole formula you're trying to prove, and put a tilde in front of that whole formula. Here's some examples.

Sentence you're trying to prove.	Wrong Assumption for IP	Right Assumption for IP
Ba	Ba	~Ba
~Nd	Nd	~ ~ Nd
Aa É Nq	~Aa É Nq	~(Aa É Nq)
Nq ^ Jc	~Nq ^ Jc	~(Nq ^ Jc)
Rt v Lm	~Rt v Lm	~(Rt v Lm)

Now ask yourself, what are the conditions that will allow you to box and cancel under indirect proof? The answer is simple. Any logical contradiction will do. You don't have to contradict your assumption (you can) but any other contradiction will do as well.

Now here's a rule that's a lot easier to understand:

Rule 6. Double Negation (Indicated by "NN")

NN allows you to do two different things.

1. Whenever any available formula begins with two negations that modify the whole rest of that formula, as in "~ ~P," you can remove those two negations to make "P".

2. You can also add two negations to any available formula "Q" to make "~ ~Q."
(The first six rules are conveniently listed on Logic Rules Sheet One)

The best way to understand a rule is to practice applying it. so here are some legitimate and illegitimate applications of NN. See if you can tell the legitimate ones from the illegitimate ones.

Can yooooooou tell the difference? You can? Great!

If you're not sure, click on the ones your not sure about to get the answer.

Here's an argument that I think is suseptible to proof using NN..

Do you believe me when I tell you this is valid? You don't? How dare you! Why I ought to ... Well, anyway, here's the truth table.

So now of course you can see it's valid! .......... hmmm. Well, just to make it a little more clear I'll just eliminate the lines where the CONCLUSION is TRUE. (Since they represent worlds where it cannot be the case where the premises are true and the conclusion is false.)

And now I'll eliminate all the lines where the premises ... er, premise are ... I mean "is" FALSE (Since those lines represent worlds where it cannot be the case where the premises are true and the conclusion is false.)

And there we are, One valid argument.

Now, how to derive it.

Well, look, we've got ~Mg as a premise, so we could have a contradiction if we had Mg to set beside it. And if we had Jr ^ Mg, we could get Mg, by simplifying the conjunction. Well, if we had ~ ~(Jr ^ Mg), we could get Jr ^ Mg from it by NN. But how to get that ~ ~(Jr ^ Mg)? I know! AIP lets us add a single snake, um, negation to the front of whatever formula we're trying to prove, and we're trying to prove ~(Jr ^ Mg), so AIP will let us write ~ ~(Jr ^ Mg). Watch.

Now let's make that assumption.

And from it get Jr ^ Mg by NN.

From this we can get Mg

Which allows us to create a contradiction by adding the premise.

Which allows us to box and cancel.

And we're done. Ta - da!

Here are three exercises you can do yourself, click on the argument for the answer.

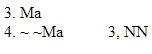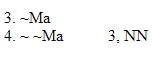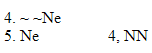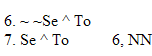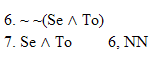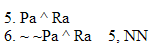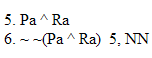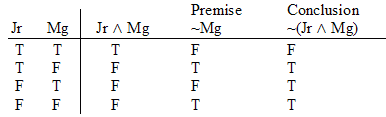
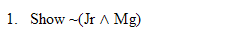
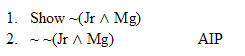
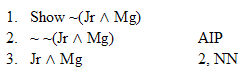
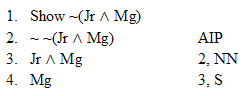
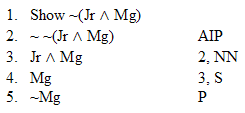
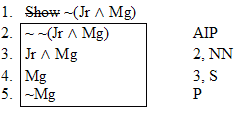
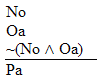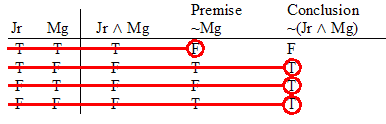
Hint. Remember AIP

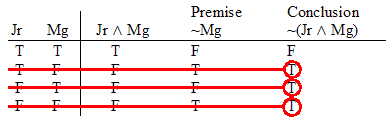
Practice 8. Use your own paper or the answer sheet at practice. For each of the following arguments, determine whether it is valid or invalid. If it's valid prove it valid by DERIVATION. If it's invalid prove it invalid by venn diagram or truth table.

1.
2.

This Site is Proudly Hosted By: