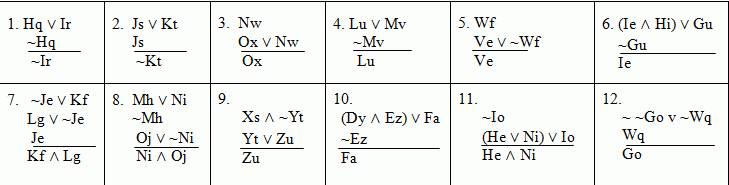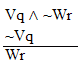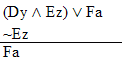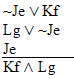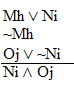Logic Chapter Nine

Logic Chapter Nine --- new
Next Chapter

Think about the following situation.You know that at least one of two alternatives (call them "P" and "Q") is true. (We write this as "P v Q" of course.) Now imagine that you find out that one of those alternatives is actually false. What does that say about the other one? Well if P is false, and P v Q is true, it follows that Q must be true. (Otherwise P v Q would be false too.) Likewise, if Q turned out to be false, P would then have to be true. This gives us a rule:

Rule 7. Disjunctive Syllogism (Abbreviated by "DS")

If a disjunction and the negation of one of its disjuncts are both available lines, the other, non-negated disjunct may be written as a new line in the derivation. Thus:

If "P v Q" and "~Q" are both available lines, then "P" may be written as a new line.

If "P v Q" and "~P" are both available lines, then "Q" may be written as a new line.

(Rules 7-13 are conveniently listed on Logic Rules Sheet Two )

And here's disjunctive syllogism in action:

Now, here's a series of arguments (which I thought were all vaild, but which aren't) of steadily increasing complexity. See how many of the valid ones you can derive!

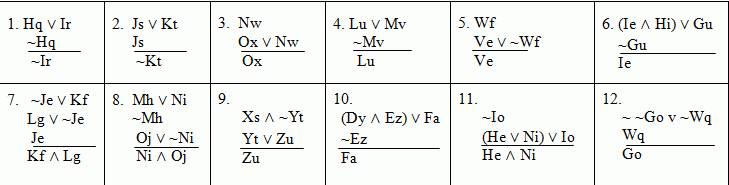
No, seriously, try to derive these arguments. (There's going to be a quiz, you know!)

If you get through with those, see which of the following are invalid, which are valid, which valid ones can be derived using DS, and which can't.

This Site is Proudly Hosted By: