Logic Chapter Ten
Next Chapter

Okay, well. Since we can take any true statement and make another true statement out of it by adding any statement we like, we can make up another rule!
 

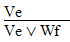
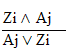
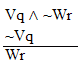
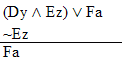
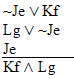
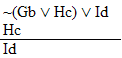
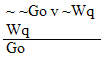
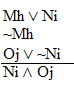
Rule 8. Addition (Abbreviated by "AD") If "P" is an available line, any formula "Q" (available or not) can be added to P by putting a wedge "v" between them to make a new sentence "P v Q" which may be written as a new line. (Rules 7-13 are conveniently listed on Logic Rules Sheet Two )

Can you figure out why these are not examples of addition?

No seriously, stop and figure out why these are not examples of addition.

They are not examples of addition because none of them take an existing formula, put a "\/" on it's right side, and then add some other random formula on the right hand side of that.

You cannot put a new formula of the left side of anything.

You cannot use the "and" symbol ("/\") in the rule addition.

You cannot apply the rule Addition inside another formula.

You can only ever do exactly what the rule allows you to no. Never anything more.

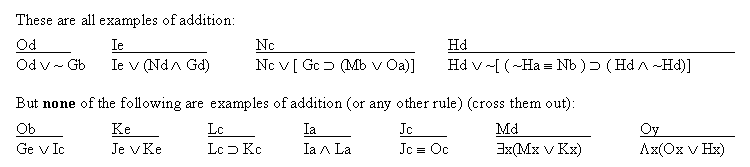
Rule 9. Commutativity (Abbreviated by "CM") If any disjunction or conjunction is an available line, then that formula may be written with the postions of its conjuncts or disjuncts reversed. (The operator may not change.) Thus: If "P ^ Q" is an available line, then "Q ^ P" may be written as a new line. If "P v Q" is an available line, then "Q v P" may be written as a new line. (Rules 7-13 are conveniently listed on Logic Rules Sheet Two )

Now, here's a series of valid arguments of steadily increasing complexity. See how many you can derive!

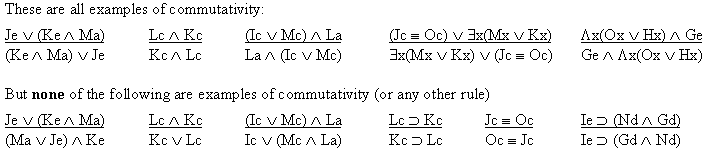
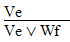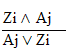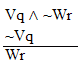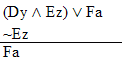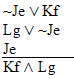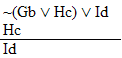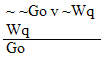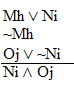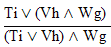As a final problem before the practice, is this argument valid or invalid?

Practice 9. Use your own paper or the answer sheet at practice. Circle the valid arguments, and cross out the invalid ones. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Derive all three of these arguments 1. 2. 3.

Copyright © 2009 by Martin C. Young

Next Chapter

---

This Site is Proudly Hosted By: