

 Ba false? Or one which makes Fe
Ba false? Or one which makes Fe (Wo
(Wo Fe) false? Now think about making one of them the the conclusion of an argument. Could you draw a picture in which the premises were true and the conclusion was false? You can't, simply because you can't ever make that concluion false. So any argument that has a tautology as it's conclusion is automatically valid!
Fe) false? Now think about making one of them the the conclusion of an argument. Could you draw a picture in which the premises were true and the conclusion was false? You can't, simply because you can't ever make that concluion false. So any argument that has a tautology as it's conclusion is automatically valid! 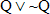 and
and 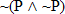 also both tautologies and they say that any formula that has the same form will also be a tautology. That's why I call them "general tautologies." ("General Tautology! The enemy is attacking!" "Hmm, that means they are trying to harm us in some way." "Well, duh. Can't you think of anything useful?" "No, I'm General Tautology, remember? I can only tell you things you could figure out for yourself." "Oh $&*#!, did I join the wrong army!")
also both tautologies and they say that any formula that has the same form will also be a tautology. That's why I call them "general tautologies." ("General Tautology! The enemy is attacking!" "Hmm, that means they are trying to harm us in some way." "Well, duh. Can't you think of anything useful?" "No, I'm General Tautology, remember? I can only tell you things you could figure out for yourself." "Oh $&*#!, did I join the wrong army!") 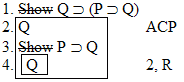
| Rule 16: Theorem (Thm <number of theorem>) If T is a theorem, containing sentence letters such as "P," "Q," "R" and so on, an "instance" of that theorem may be written in as a new line in which every "P" has been replaced by exactly the same sentence, every "Q" has been replaced by exactly the same sentence (which can be different from the sentence written in for every "P"), and so on. |
 Ni, or (Ja v Te) ^ (Wf
Ni, or (Ja v Te) ^ (Wf  Tm]).
Tm]).  P
P Ba
Ba Rs
Rs (Hi ^ Gu)
(Hi ^ Gu) (Mu v No)
(Mu v No) (Iu
(Iu  Ni)
Ni) (He
(He Ni)
Ni) Tm])}
Tm])} {(Ja v Te) ^ (Wf
{(Ja v Te) ^ (Wf  Tm])}
Tm])} (P
(P  Q)
Q)  (Ba
(Ba Rs)
Rs) ((Hi ^ Gu)
((Hi ^ Gu)  (Mu v No)
(Mu v No) ((Mu v No)
((Mu v No) (Iu
(Iu  ({(Ja v Te) ^ (Wf
({(Ja v Te) ^ (Wf  Tm])}
Tm])} Ba )
Ba ) Tm])}
Tm])} ([He
([He Ni]
Ni] {(Ja v Te) ^ (Wf
{(Ja v Te) ^ (Wf  Tm])})
Tm])}) (Ba
(Ba Rs) with the theorem's operators marked:
Rs) with the theorem's operators marked:
| Rs |  |
( | Ba |  |
Rs | ) |
| Rs |  |
( | Ba |  |
Rs | ) |
| Rs |  |
( | Ba |  |
Rs | ) |
 (P
(P  Q).
Q).| (Mu v No) |  |
( | (Hi ^ Gu) |  |
(Mu v No) | ) |
| (Iu |
 |
( | (Mu v No) |  |
(Iu |
) |
| Ba |  |
( | {(Ja v Te) ^ (Wf  Tm])} Tm])} |
 |
Ba | ) |
{(Ja v Te) ^ (Wf  Tm])} Tm])} |
 |
( | [He Ni] Ni] |
 |
{(Ja v Te) ^ (Wf  Tm])} Tm])} |
) |
 P) from the things that are not instances of theorem 1.
P) from the things that are not instances of theorem 1.
| 1. | (Hi  Gu) Gu) (Hi ^ Gu) (Hi ^ Gu) |
Instance | Not Instance |
| 2. | (Hi  Gu) Gu) (Hi (Hi  Gu) Gu) |
Instance | Not Instance |
| 3. | (Mu ^ No)  (Mu v No) (Mu v No) |
Instance | Not Instance |
| 4. | [Rs  (Ba (Ba Rs)] Rs)] [Rs [Rs (Ba (Ba Rs)] Rs)] |
Instance | Not Instance |
| 5. | {(Mu v No)  [(Hi ^ Gu) [(Hi ^ Gu)  (Mu v No)]} (Mu v No)]} {(Mu v No) {(Mu v No) [(Hi ^ Gu) [(Hi ^ Gu)  (Mu v No)]} (Mu v No)]} |
Instance | Not Instance |
| 6. | Ba  Rs Rs |
Instance | Not Instance |
| Theorems 3 & 4 (Exportation Laws) 3. [(P ^ Q)  R] R]  (Q (Q R)] R)]4. [(P ^ Q)  R] R]  (P (P R)] R)] |
 (Q
(Q R)]
R)]  R] says almost exactly the same thing as theorem 3, it is not theorem 3 and no instance of this particular formula will ever be an instance of theorem 3.
R] says almost exactly the same thing as theorem 3, it is not theorem 3 and no instance of this particular formula will ever be an instance of theorem 3. R]" is logically equivalent to "[(P
R]" is logically equivalent to "[(P  (Q
(Q R)]," which just means that whenever "[(P ^ Q)
R)]," which just means that whenever "[(P ^ Q)  R]" is true, "[(P
R]" is true, "[(P  (Q
(Q R)]" will also be true, and vice versa, which, of course implies that whenever "[(P ^ Q)
R)]" will also be true, and vice versa, which, of course implies that whenever "[(P ^ Q)  R]" is false, "[(P
R]" is false, "[(P  (Q
(Q R)]" will also be false, and vice versa.
R)]" will also be false, and vice versa. 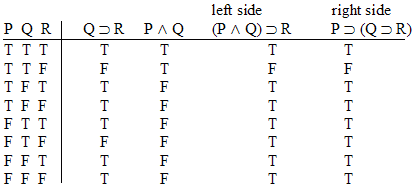

 R]
R]  (P
(P R)].
R)].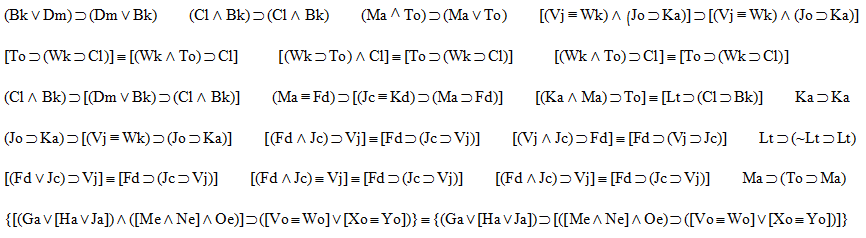
1. 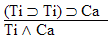 |
2. 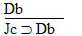 |
3. 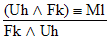 |
4. 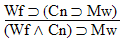 |
5. 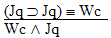 |
6. 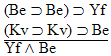 |
7. 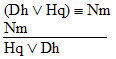 |
8. 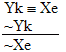 |
9. 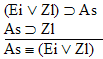 |
10. 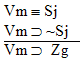 |
11. 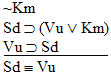 |
12. 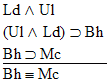 |
13. 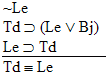 |
14. 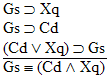 |
15. 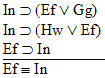 |
16. 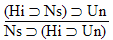 |
17. 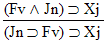 |
18. 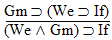 |
19. 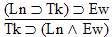 |
20. 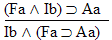 |
|
