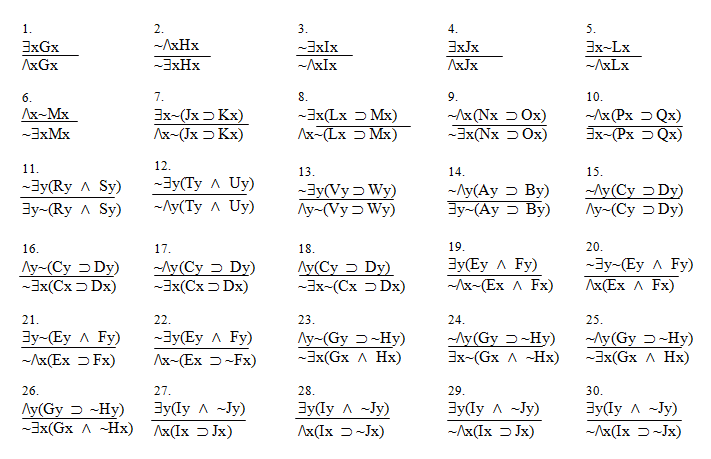1. If "
2. If "~
3. If "
4. If "~
5. If "
6. If "~
7. If "
8. If "
| Rule 17: Change Quantifier (CQ) Comes in eight little rules. 1. If " 2. If "~ 3. If " 4. If "~ 5. If " 6. If "~ 7. If " 8. If " |
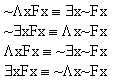
 |
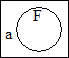 |
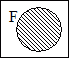 |
 |
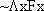 and
and 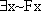 true, one makes both
true, one makes both 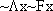 and
and 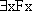 true, one makes both
true, one makes both 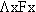 and
and 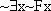 true and one makes both
true and one makes both 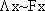 and
and 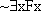 true. Which one is which?
true. Which one is which? 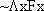 and
and 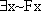 false, one makes both
false, one makes both 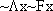 and
and 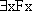 false, one makes both
false, one makes both 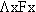 and
and 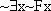 false and one makes both
false and one makes both 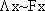 and
and 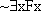 false. Which one is which for falsity?
false. Which one is which for falsity?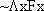 and
and 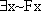 have different truth values? Can you find a picture in which
have different truth values? Can you find a picture in which 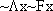 and
and 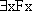 have different truth values? Is there one in which have
have different truth values? Is there one in which have 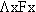 and
and 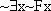 different truth values? Or can you find a picture in which
different truth values? Or can you find a picture in which 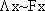 and
and 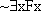 have different truth values?
have different truth values?