|
|
All things in the universe are bullfrogs | |
|
|
At least one camel exists | |
| |
It's not true that everything in the universe is a bullfrog | |
| |
Not even one aardvark exists |
|
Ax:
Bx: Cx: d: e: f: |
x
is an aardvark x is a bullfrog x is a camel Dick Cheney Emo Phillips Francis the talking mule |
|
|
All things in the universe are bullfrogs | |
|
|
At least one camel exists | |
| |
It's not true that everything in the universe is a bullfrog | |
| |
Not even one aardvark exists |
 |
 |
 |
 |
|
| A bullfrog exists | is made true by |  |
See the "k" (whatever "k" stands for) in the bullfrog space | |
| All things are aarrdvarks | is made false by |  |
See the "b" (whatever "b" stands for) in the non-aardvark space |
| A bullfrog exists | is made false by |  |
Notice the bullfrog space is empty. | |
| All things are aardvarks | |
is made true by |  |
Notice the non-aardvark space is empty. |
| This formula: | Is made true by: | And made false by: |
| |
 |
 |
|
|
 |

|
|
|
 |

|
|
|
 |

|
|
|
 |

|
|
|
 |

|
|
|
 |
 |
This formula: |
Is made true by: |
And made false by: |
|
|
 |
 |
This formula: |
Is made true by: |
And made false by: |
|
|
 |
 |
This formula: |
Is made true by: |
And made false by: |
|
|
|
 |
This formula: |
Is made true by: |
And made false by: |
|
|
|
 |
| |
|
|
|
|
|
|
||
|
|
|
|
| |
|
|
|
| |
|
||
| |
|
|
| Keith is hairy Mike is insane Ossie is hairy No-one is green |
 |
is proved invalid by |  |
| Jeff is green Ossie is green Everything is green |
 |
is proved invalid by |  |
| Jeff is not a kangaroo A kangaroo exists |
|
is proved invalid by |
 |
| Nigel is an elk A non-elk exists |
|
is proved invalid by |
 |

 |
Is Is ~ |
 |
Is Is ~ |
 |
Is Is ~ |
 |
Is Is ~ |
 |
Is ~ Is |
 |
Is ~ Is |
 |
Is ~ Is |
 |
Is ~ Is |
| Rule 17: Change
Quantifier (CQ) Comes in eight little rules. 1. If " 2. If "~ 3. If " 4. If "~ 5. If " 6. If "~ 7. If " 8. If " |
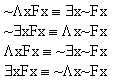
 |
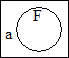 |
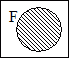 |
 |
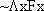 and
and 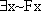 true, one makes both
true, one makes both 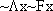 and
and 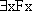 true, one makes both
true, one makes both 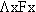 and
and 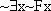 true and one makes both
true and one makes both 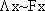 and
and 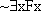 true. Which one is which?
true. Which one is which? 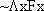 and
and 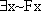 false,
one makes both
false,
one makes both 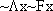 and
and 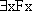 false,
one makes both
false,
one makes both 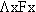 and
and 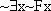 false and one makes
both
false and one makes
both 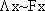 and
and 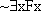 false. Which one is which for falsity?
false. Which one is which for falsity?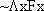 and
and 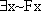 have different
truth values? Can you find a picture in which
have different
truth values? Can you find a picture in which 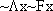 and
and 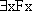 have
different truth values? Is there one in which have
have
different truth values? Is there one in which have 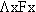 and
and 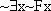 different truth
values? Or can you find a picture in which
different truth
values? Or can you find a picture in which 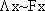 and
and 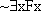 have
different truth values?
have
different truth values?  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Homework
12. Use your own paper or the answer sheet at logic13homework.rtf. For each of the following arguments do TWO things. First, translate it into English based on the following scheme.
Second, circle it if it's valid, cross it out if it's invalid.
|
