The existential operator allows us to say that something does or doesn't exist.
The universal operator allows us to make claims about properties objects have to have.
The cool thing about these operators is that our language is suddenly much more powerful. The bummer is that truth tables can't help us very much with existential and universal statements.
With those operators, and this scheme:
|
Ax:
Bx: Cx: d: e: f: |
x is an aardvark x is a bullfrog x is a camel Dick Cheney Emo Phillips Francis the talking mule |
We can say things like:
 |
All things in the universe are bullfrogs | |
 |
At least one camel exists | |
 |
It's not true that everything in the universe is a bullfrog | |
 |
Not even one aardvark exists |
A statement in which the universal operator is the main operator is a "universal statement." (Or just a "universal.")
A statement in which the existential operator is the main operator is a "existential statement." (Or just an "existential.")
And of course, a statement in which the negation operator is the main operator is a "negation."
So this means that one of the above statements is an existential statement, one is a universal statement, and two of them are negations.
Here are some statements you can practice translating. Don't worry if I've worded the translation differently from you. As long as the idea is the same, you're fine. (Answers at bottom of this page.)
|
||||
|
||||
|
Write down what you think each sentence means before you click on it to see the answer. Be careful! Look at where the parentheses are before you decide what a statement means.
As you can probably guess, there are weirdnesses involved with these two operators. The existential weirdness doesn't really show itself until we get into the rules for creating existential statements, but the universal weirdness shows up right away.
Before we get weird, let's expand our world-construction system. We will represent a whole universe as a rectangle
and empty space by cross hatching 
so that, for instance, the picture 
would represent a completely empty universe.
Now, on to the universal weirdness.
The classic universal statement is "all men are mortal." Well, that's boring, so I'll use the statement "all badgers are Corsican" because I like badgers, and Corsica is cool. Using one of our powerful new operators, we can symbolize the statement "all badgers are Corsican" as
which more precisely says that "if something is a badger then it's Corsican." Right away, the weirdness starts, because this statement, "all badgers are Corsican" doesn't actually say that any badgers exist! It just says that if any badgers do happen to exist, then all of them are Corsican. So the statement is made true by all the following universes
 |
 |
 |
 |
|
true if and only if it makes it impossible for an object to turn up that makes false. And can only be false if there is some object that is a badger but not a Corsican. So if you rule out the possibility that an object can turn up inside the B circle but outside the C circle, you've made true, no matter what other properties that universe may have. Now lets look at these universes individually. The first one is easy. Here is a universe that may or may not be empty but, if any badgers do happen to exist here they will perforce have to be Corsican because the B circle is completely inside the C circle. So no B circle objects can be outside the C circle, and
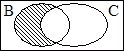
has to be true. The second one is also easy. Here there is a part of the B circle that's outside the C circle, but it doesn't matter because that part of the B circle is crosshatched, which defines it as empty, so no non-empty part of the B circle is outside the C circle, so no non-Corsican badgers can exist, and
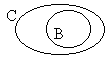
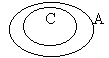
is true. The third one is a little trickier. You can't see the C circle here because it exactly follows the line of the edge of the universe. In this universe, everything is Corsican, so if any badgers do happen to exist, they're Corsican too. So
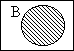
is true here too. The fourth universe is where the weirdness really kicks in. It is a universe bereft of badgers. No badgers here exist because the B circle is defined as empty. Since no badgers whatsoever exist, it is absolutely imposible for a badger to exist that is not a Corsican. Since no non-Corsican badger can exist,
cannot be made false. If cannot be made false, then perforce it is true.The fifth, totally empty universe has exactly the same property. Badgers cannot exist in it, so non-Corsican badgers cannot exist, so
is true. So it's important to remember that universal statements don't say anything about what does or does not exist. In a completely empty universe, the statement "all things are bullfrogs" is true even though no bullfrogs actually exist, because nothing else exists either. Thus the statement "all things are bullfrogs" is logically equivalent to "nothing exists that is not a bullfrog" or "if anything exists, it's a bullfrog." Existential statements on the other hand always assert that something exists or does not exist. Negations, as always, say that whatever follows the negation operator is not true.
Now, we can make some universal and existential statements true or a false with our regular old pictures. For instance:
| A bullfrog exists |  |
is made true by |  |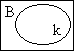
See the "k" (whatever "k" stands for) in the bullfrog space |
| All things are aarrdvarks |  |
is made false by |  |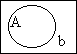
See the "b" (whatever "b" stands for) in the non-aardvark space |
But to say more we need the new stuff.
| A bullfrog exists | |
is made false by | |
Notice the bullfrog space is empty. |
| All things are aardvarks | |
is made true by |  |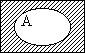
Notice the non-aardvark space is empty. |
Here's it all put together with some more formulas.
| This formula: | Is made true by: | And made false by: |
|
|
|
|
|
|
|
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
 |
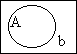
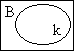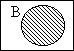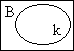
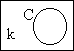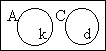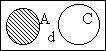
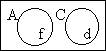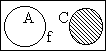
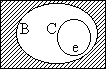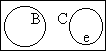Here are some more difficult ones. We'll do more with these next lesson.
This formula: |
Is made true by: |
And made false by: |
|
|
|
 |
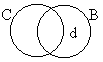This formula: |
Is made true by: |
And made false by: |
 |
 |
 |
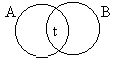This formula: |
Is made true by: |
And made false by: |
 |
 |
 |
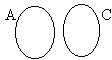This formula: |
Is made true by: |
And made false by: |
 |
 |
 |
For practice, cover the answers given above and, for each statement given below, draw a world that makes that statement true.
|
|
|
|
|
|
|
|
|
|
|
|
|
After checking your answers, cover them again, and for each statement, draw a world that makes that statement false.
| |
|
|
|
|
|
|
|
|
|
|
|
1. Everything is an aardvark.
2. A bullfrog exists.
3. No bullfrogs exist.
4. Not everything is a camel.
5. Dick Cheney is a camel and an aardvark exists.
6. A camel exists or Francis the talking mule is an aardvark.
7. If Emo Phillips is a camel then everything is a bullfrog.
8. All bullfrogs are camels.
9. No aardvarks are bullfrogs.
10. Some camels are aardvarks
11. Some camels are not aardvarks
Copyright © 2009 by Martin C. Young
Next Chapter
This Site is Proudly Hosted By:
